Problema 4 de la fase catalana de la 57 Olimpiada Matemática Española (2020/21)
Se dirige a una edad de: 16-17 años

Determina todos los valores enteros de n tales que la fracción (8n – 3)/(17n – 9) es irreducible.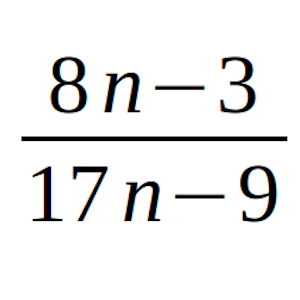
Solución:

Tanteando no llegamos a ningún lado, aparentemente.

Si combinamos el denominador y el denominador, puede que tengamos una expresión que nos permita razonar mejor, ya que 17(8n – 3)/(17n – 9) – 8 = (17·8·n – 51 – 8·17·n + 72)/(17n – 9) = 21/(17n – 9). Si la fracción que nos ocupa es irreducible, la otra también lo será, ya que no es posible que se simplifique el valor primo 17 que es el número por el que la hemos multiplicado.

Así, vemos que para que sea reducible la fracción no hay más remedio que sea divisible por 3 o por 7, por lo que sólo debemos buscar cuándo 8n – 3 es múltiplo de 3 y también 17n – 9, y cuando sucede lo mismo con 7.

Razonando con 3, 8n – 3 es múltiplo de 3 si y sólo si 8n lo es, luego n es múltiplo de 3, y entonces 17n – 9 también es múltiplo de 3, por lo que siempre que n sea múltiplo de 3, la fracción es reducible.

Razonando con 7, 8n – 3 es múltiplo de 7 si y sólo si n – 3 es múltiplo de 7, es decir, n es de la forma 7k + 3. En ese caso, 17·(7k + 3) – 9 = 119k + 51 – 9 = 119k + 42 = 7(17k + 6), es decir, 17n – 9 es múltiplo de 7 también.

Por lo tanto, la fracción (8n – 3)/(17n – 9) es irreducible para cualquier n que cumpla que no sea múltiplo de 3 ni sea divisible por 7 al restarle 3.

Posibles valores para n serían 1, 2, 4, 5, 7, 8, 11, 13, 14, 16, 19, 20, 22, 23, 25, 26, 28, 29, 32, 34, … Se da la circunstancia que cada 21 números vuelve a repetirse la misma secuencia de valores n a partir de la cual obtenemos fracciones irreducibles.