Problema 2 del nivel C fase comarcal de Alicante de la Olimpiada de la Comunidad Valenciana 2021 Se dirige a una edad de: 10-11 años
El coste de una llamada telefónica depende del tiempo de comunicación y de la distancia.
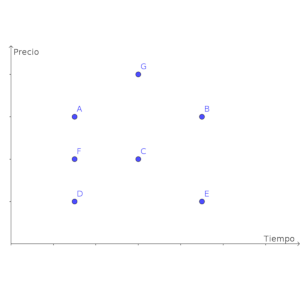
En la gráfica siguiente se han representado las llamadas hechas por cinco personas, A, B, C, D y E.
Observa la gráfica (que representa el precio frente al tiempo) y responde:
a) ¿Quién ha llamado más lejos?
b) ¿Quién ha llamado más cerca?
c) ¿Qué llamadas se han realizado a la misma distancia?
d) ¿Dónde situarías una llamada hecha a la misma distancia que F, pero de duración doble?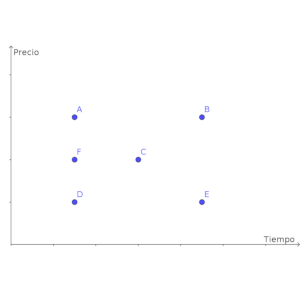
Solución:
Se trata de representar la información. Aunque se da por sentado, tal vez en el enunciado deberíamos advertir que el coste depende proporcionalmente de ambos factores, ya que si no la representación podría dar información escasa, sobre todo para la pregunta tercera y la cuarta.
La respuesta a la pregunta a) es la A, ya que es una de las llamadas más caras, junto a la B, pero la B dura más, de forma que la A se a hecho más lejos. Además, puesto que no hay llamadas más cortas, las demás han debido realizarse a lugares más cercanos.
La respuesta a la b) es, por el contrario, la E, ya que es una de las más baratas, junto a la D, pero ha durado más.
La pregunta c) es más complicada, ya que no sabemos cuánto influye cada factor. Suponiendo que a doble duración corresponde doble tiempo (proporcionalidad), parece que D, B y C están hechas al mismo lugar, ya que C y B duran el doble y el triple respectivamente que D, y también cuestan el doble y el triple.
La gráfica para responder a la pregunta d) sería la imagen siguiente, de nuevo suponiendo que doble duración supone el doble de coste. Estaría el doble de alto que F, y también el doble de desplazada a la derecha (sobre la C).