Problema 4 del nivel A fase comarcal de Alicante de la Olimpiada de la Comunidad Valenciana 2021 Se dirige a una edad de: 12 - 13 años
Uniendo los puntos medios de un hexágono regular, obtenemos un hexágono regular girado, y si unimos los puntos medios de los lados de este hexágono girado, obtenemos un hexágono como el primero, pero más pequeño, como vemos en la imagen.
¿Puedes decir cuánto más pequeño es?
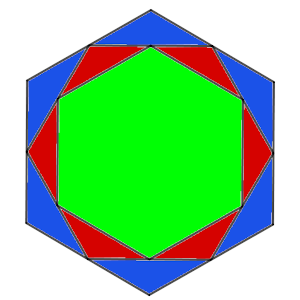
Solución;
La clave en los problemas en los que sale un hexágono regular es trabajar con triángulos regulares, dividiendo desde el centro.
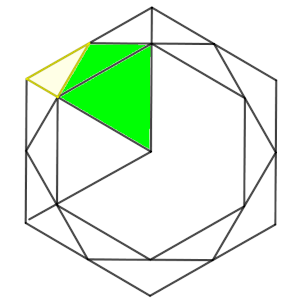
Evidentemente, la primera vez que reducimos el tamaño del hexágono, quitamos a cada uno de los triángulos regulares dos trozos. Como los ángulos del borde del hexágono inicial eran de 120º (dos triángulos equiláteros), resulta que los dos trozos que le quitamos tienen la forma de medio triángulo equilátero, y su lado medirá exactamente la mitad que los del triángulo inicial.
Puesto que un triángulo equilátero se puede dividir en cuatro triángulos que miden la mitad del lado, en realidad le estaremos quitando a cada triángulo una cuarta parte del área, es decir, que el área de todo el hexágono estará multiplicada por ¾.
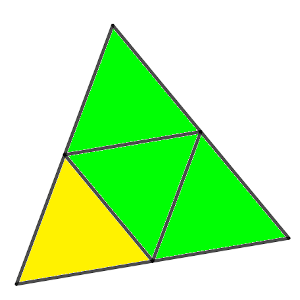
Y eso quiere decir, que el segundo hexágono, respecto del primero, estará multiplicado por 9/16, lo que significa multiplicar por 0,5625, es decir, que el área del hexágono pequeño será un 56,25% del grande, algo más de la mitad.
Otra manera de verlo nos la ha dado @M1GU3L_HH en twitter, con este dibujo:
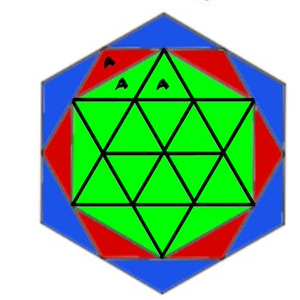
Otra forma de llegar al mismo resultado es encontrar que la relación entre los lados de cada hexágono adyacente es cos(30º).