Problema 4 del nivel B fase comarcal de Alicante de la Olimpiada de la Comunidad Valenciana 2021
Se dirige a una edad de: 14 - 15 años

Una urna contiene tres bolas blancas y cuatro rojas.

Transferimos tres bolas elegidas al azar a una segunda urna vacía.

Seleccionamos una bola al azar y resulta ser blanca.

¿Cuál es la probabilidad de que, al extraer las dos bolas que quedan en la segunda urna, resulte que cada una es de un color?

Solución:

Este ejercicio fue especialmente complicado, ya que el escenario incluía un proceso complejo y unas restricciones importantes.

He tratado de analizarlo de forma sencilla, pero no he conseguido nada razonable. Vamos a tratar de hacer el procedimiento complejo.

Deberíamos primero elegir la configuración de las tres bolas de la segunda urna, luego elegir una de estas tres primero y luego las otras dos. Seis ramas en total. Pero vamos a pararnos en la cuarta rama, y tomar sólo aquellas en las que es blanca, ya que sabemos lo que ha ocurrido, es decir, descartamos las que no han ocurrido.

Lo primero que hay que hacer es que sólo nos valen aquellas ramas del árbol de sucesos en las que la cuarta opción haya sido blanca, despreciando las otras. Así, la probabilidad total ya no sumará 1, ya que algunas ramas, que son posibles, no han ocurrido. Eso significa que deberemos ver cuál es la nueva probabilidad total, y dividir por ella para que analicemos cuál es la probabilidad de lo que buscamos del total de casos.

Ante varios comentarios, he revisado lo que ponía la solución y estaba completamente equivocada, así que paso a corregir, desde la imagen del árbol a todo lo que hay a continuación. el problema es que puse menos bolas blancas de las que había en el problema.

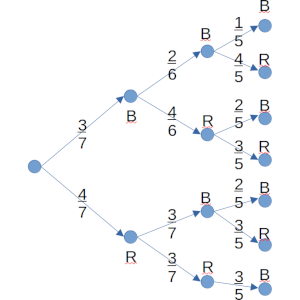
En cada una de las 7 ramas que dibujo se puede obtener una bola blanca, pero la probabilidad en cada caso es diferente:

BBB: 6/210
BBR: 24/210
BRB: 24/210
BRR: 36/210
RBB: 24/210
RBR: 36/210
RRB: 36/210

Ahora, añadiendo que en efecto se saque una bola blanca, se ajusta aún más la probabilidad:

BBBB: 6/210
BBRB: 16/210
BRBB: 16/210
BRRB: 12/210
RBBB: 16/210
RBRB: 12/210
RRBB: 12/210

Evidentemente, esta probabilidad se obtiene sumando todas las ramas, y es un total de 90/210 = 3/7.

Eso quiere decir que de cada 7 veces que intentemos hacer el experimento, en 3 obtendremos una bola blanca, que es la situación que nos interesa.

Ahora, vamos a ver qué nos pide realmente el problema, y es ver en cuáles de esos 90 casos quedan dos bolas de diferente color, que serían los casos (2) (3) y (5), en los cuales la probabilidad es de 16/210 en cada uno de ellos, por lo que tendríamos en total una probabilidad de 48/210.

Por lo tanto, la probabilidad de que las otras dos fuesen de diferente color sería de 48/90 = 8/15 = 0.533.

Por tanto, en contra de lo que afirmaba en la redacción anterior, si se hiciese el experimento suficiente número de veces, algo más del 53% de los casos en los que saliera la bola blanca, las otras dos serían de diferente color.