Problema 1 del concurso Olitele 2021 Se dirige a una edad de: 16-17 años
Tenemos un tablero cuadrado 5×5 y las 5 piezas en forma de “L” (excepto una que es un cuadrado) que se muestran:
Hay muchas maneras de situar las piezas de forma que llenen el tablero, se muestran tres ejemplos.
a) Determina de cuántas formas diferentes se pueden situar las cinco piezas para llenar el tablero, que siempre consideramos con la misma orientación (la pieza cuadrada no se distingue si está girada o no, así que siempre se considera que está puesta de la misma forma salvo que cambiemos su ubicación).
b) ¿En cuántas de las ocasiones la pieza cuadrada queda situada exactamente en el centro?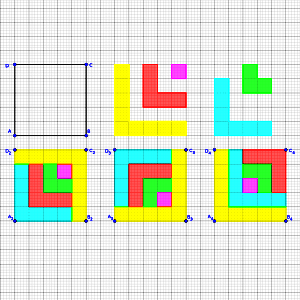
Solución:
Claramente se trata de un problema de combinatoria, que hay que resolver pacientemente.
Los términos pertenecen a una sucesión, así que podemos tratar de resolverlos por inducción, referenciando siempre de un término a otro.
Lo más rápido, para abordar el apartado (a) es tratar de colocar primero la pieza mayor, cosa que sólo podremos hacer de 4 formas, y nos quedará una zona 4×4 para cubrir con las otras 4 piezas.
Así, que si damos con el número de formas en las que podemos situar las 4 piezas y les llamamos F4, el número total de formas para colocar las 5 cumplirá F5 = 4·F4.
De forma similar, tenemos que F4 = 4·F3, que F3 = 4·F2, y por tanto, como F1 (formas de llenar un cuadrado con el cuadrado) según el enunciado es 1, tenemos que F5, que es el número que buscamos, será 4⁴ = 64.
Para el apartado (b) parece lógico tratar de hacer algo similar, pero iniciando el proceso desde la zona menor hacia arriba, ya que ahora sabemos que el centro está ocupado por el cuadrado de lado 1.
Eso significa que disponemos de 4 formas de poner la pieza de tamaño siguiente (la verde en la imagen), y son simétricas.
Observamos que poner la última pieza es trivial si hemos dejado sitio: sólo tendremos un hueco.
Ahora, podemos poner la pieza siguiente de 4 formas también, pero cambia mucho que la pongamos en un sitio u otro, porque si estamos demasiado cerca del borde, limitaremos el espacio para poner la siguiente pieza. Distinguiremos 4 grupos en los 16 casos que tenemos hasta ahora.
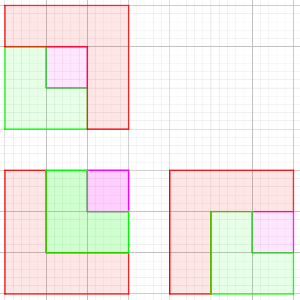
Distinguimos 3 casos en especial dentro de esos 4 grupos.
Si ponemos la pieza roja sin ningún contacto con el cuadrado central (4 casos), tocamos dos bordes, con lo que sólo hay 1 forma de situar la azul.
Si la ponemos de forma que tenga un único contacto con un borde del cuadrado central (8 casos), con lo que toca un único borde exterior, entonces hay 2 formas de situar la azul (hay que tener en cuenta que hay que dejar sitio para la grande), por lo que tendremos 16 formas más de completar.
Por último, si ponemos la pieza roja en el lado opuesto de la verde, con dos lados en contacto con la pieza central (4 casos), entonces dejamos mucho sitio para poner la pieza azul, tenemos 4 formas de colocarla. Por eso añadimos otras 16 formas.
En total, tenemos 16 + 16 + 4 = 36 formas diferentes en las que la pieza cuadrada queda exactamente en el centro.