Problema 4 del concurso Olitele 2021 Se dirige a una edad de: 16-17 años
Una antena de telefonía se fija verticalmente sobre una base rectangular horizontal, de vértices ABCD, con cables que van desde el extremo superior de la antena a los cuatro vértices de la base.
Conocemos la longitud de tres cables, que son:
El cable que va del vértice A a la antena, que tiene a metros.
El cable que va del vértice B a la antena, que tiene b metros.
El cable que va del vértice C a la antena, que tiene c metros.
Estos tres datos permiten determinar la longitud del cuarto cable, que se une al vértice D. Calcula, en función de a, b y c, la longitud del cable que falta.
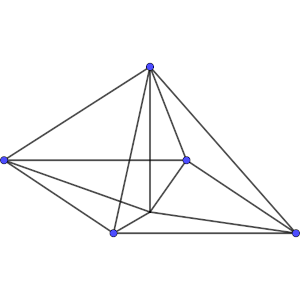
Solución:
Y llegamos a un problema de geometría tridimensional.
Hay varias formas de tratar de resolverlo, que se basan en que la antena tendrá una determinada altura y estará situada en un punto determinado, puede que sea el centro o no del rectángulo (si lo fuese a, b y c serían iguales), y que la antena es perpendicular al rectángulo.
Cada persona que participaba en el concurso obtenía un juego de datos diferente, de forma que la respuesta debía estar personalizada (no era con fórmulas).
Podemos aplicar el Teorema de Pitágoras a los datos, o bien estudiar todo el problema con coordenadas tridimensionales.
Veamos el estudio con coordenadas. Supongamos que las longitudes del rectángulo son x e y (las cuatro coordenadas pueden ser A(0, 0, 0), B(x, 0, 0), C(x, y, 0) y D(0, y, 0)), y las coordenadas del extremo superior de la antena son P(z, t, u), con u > 0.
Los datos que tenemos son d(A, P) = a, d(B, P) = b, d(C, P) = c, y lo que debemos averiguar es d(D, P).
Situando los datos de forma polinómica, a² = z² + t² + u², b² = (z – x)² + t² + u², c² = (z – x)² + (t – y)² + u². El objetivo es conocer d² = z² + (t – y)² + u².
Restando las dos primeras igualdades (ya que son muy parecidas), tenemos que a² – b² = z² – (z – x)² = x² + 2zx. Sin embargo, de la misma forma, viendo puesto que la tercera igualdad y el objetivo son también muy parecidas, tenemos que d² – c² = z² – (z – x)² = x² + 2zx = a² – b².
Puesto que a, b y c son conocidos, tenemos que d² = a² – b² + c², de donde podemos calcular d mediante la raíz cuadrada: d = raíz(a² – b² + c²).