Problema 2 de la Fase Local de la Olimpiada Española de Matemáticas 2022 (viernes mañana) Se dirige a una edad de: 16-17 años
Sea ABC un triángulo isósceles con el ángulo BAC de 100º.
La bisectriz del ángulo CBA corta al lado AC en el punto D.
Demostrar que BD + DA = BC.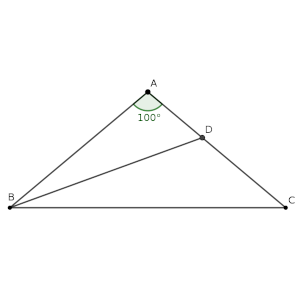
Solución:
Los problemas de geometría suelen ser todo un reto en este nivel.
Veamos dos formas diferentes de solucionar el problema y hacer la demostración.
Una de ellas es más estándar, es decir, se debería poder hacer en cualquier caso. Completamos los ángulos que hay en el dibujo, y tenemos dos triángulos adyacentes, el ABD y el BDC, que comparten el lado BD.
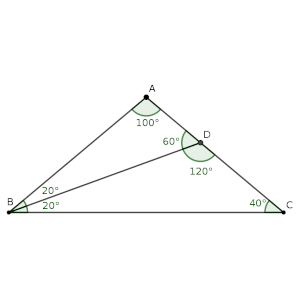
Aplicando el Teorema del seno, podemos relacionar BD con todos los lados implicados en la igualdad que queremos probar, ya que BD/sen(40) = BC/sen(120º).
BC = sen(120º)BD/sen(40º) = sen(60º)BD/sen(40º).
Veamos ahora cómo representar la otra parte de la igualdad, a ver si da lo mismo.
BD/sen(100º) = DA/sen(20º), de forma que DA = sen(20º)BD/sen(100º) .
Por lo tanto, BD + DA = BD + sen(20º)BD/sen(100º).
Reduciendo a denominador común, tenemos que BD + DA = BD(sen (100º) + sen(20º))/sen(100º).
Ahora, basta comprobar que estas dos fracciones son iguales: (sen (100º) + sen(20º))/sen(100º) y sen(60º)/sen(40º).
Para eso, hay que transformas la suma de senos en producto (sen(100º) + sen(20º)) = 2sen(60º)cos(40º) para poder simplificar, y usar que sen(80º) = 2sen(40º)cos(40º) (fórmula del ángulo doble).
Entonces queda BD + DA = BD(sen (100º) + sen(20º))/sen(100º) = BD(2sen(60º)cos(40º))/(2sen(40º)cos(40º)) = BD(sen(60º)/sen(40º)) = BC, como queríamos demostrar.
Nota: en un momento determinado, sentimos la tentación de cambiar sen(100º) por sen(80º), pero el resultado no se puede simplificar, y por tanto tuve que volver atrás y deshacer el cambio.
La otra forma de enfocar el problema es más geométrica, requiere un poco más de creatividad y resulta mucho más atractivo.
La clave es empezar de la misma forma, poniendo ángulos, y descubrimos que hay un ángulo de 60º, ¡como en un triángulo equilátero!
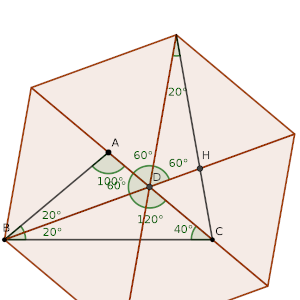
Ahora, para poner esa longitud AD en línea recta con BD para poder sumarlo, podemos dibujar seis triángulos equiláteros y repetir la construcción en el que haría que estuviese sobre la misma recta que BD.
Dada la simetría de la figura, está claro que la prolongación del segmento que pasa por el punto H (y que se ha usado para trazarlo) pasa también por C, ya que esta línea, que forma un ángulo de 20º con uno de los lados de uno de los triángulos, es simétrica respecto a la recta que incluye AC (y C está sobre el eje de simetría).
Esa simetría hace que el ángulo DCH sea 40º, por lo que podemos completar los ángulos que quedan.
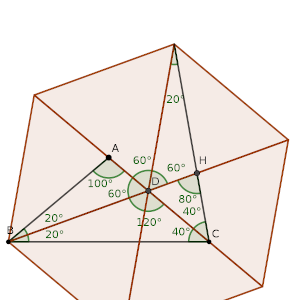
Pero si observamos el triángulo BHC, se aprecia que tiene dos ángulos iguales, por lo que es realmente isósceles, y por tanto se tiene que BD + DH = BD + AD = BC.
Geometricamente, más sencillo, tomamos un punto E, sobre BC tal que BD=BE. Se forman dos triángulos isosceles uno de los cuales, EDC es semejante al triángulos ABC original. Razonando quecla bisectriz determina sobre el lado segmentos proporcionales a los otros dos lados se termina en cuatro líneas el razonamiento.