Problema 8 del concurso Olitele 2021 Se dirige a una edad de: 16-17 años
En una circunferencia de radio R trazamos una una circunferencia tangente a la circunferencia y al diámetro, que vemos en este caso de color rojo. Su radio será r.
Seguro que sabemos deducir que el radio de esta circunferencia es r = R/2.
A continuación trazamos una circunferencia de radio s tangente a la circunferencia de color rojo, al diámetro y a la circunferencia inicial, en el dibujo de color azul. Se pide como primer dato la relación entre s y R, es decir, el valor k que cumple s = k·R.
Por último, trazamos una circunferencia de radio t, tangente a la circunferencia de radio s anterior, al diámetro y a la circunferencia inicial, que en el dibujo vemos de color naranja. Se pide la relación entre t y R, es decir, el valor h que cumple t = h·R.
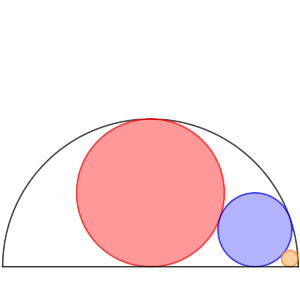
Solución:
Lo primero que tenemos que hacer es construir toda la figura a tamaño fijo, es decir, escalar el radio de la circunferencia inicial para que nos salgan números concretos en lugar de proporcional a R. Yo voy a usar radio 1, pero si no queremos que nos salgan fracciones, podemos optar por tomar valores que nos permitan dar números enteros, multiplicando todos los números que nos vayan saliendo por un factor adecuado según los vayamos obteniendo.
Voy a poner la circunferencia inicial centrada en el punto (0,0) y su diámetro sobre el eje x, para simplificar los cálculos.
Evidentemente el radio de la primera circunferencia es ½ (por ejemplo, aquí podríamos duplicar el radio inicial, que el radio inicial sea 2 y entonces sería 1 el de la primera circunferencia), ya que al ser tangente a la circunferencia contenedora, y pasar por el centro la otra tangente al diámetro por simetría, se da que 2r = 1.
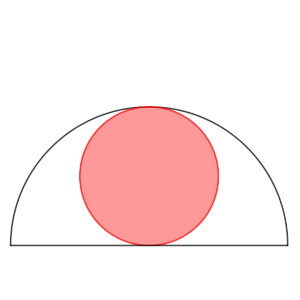
Ahora, si el centro de la segunda circunferencia tiene las coordenadas (x, s), está claro que s debe ser el radio para que siga siendo tangente al diámetro inicial, pero al unir el punto de tangencia con ambos radios de las circunferencias, los radios deben estar sobre la misma recta, por ser perpendiculares al punto de tangencia. Así, se forman unos vectores que podemos caracterizar por su tamaño.
En efecto, (r + s)² es la “hipotenusa” del triángulo rectángulo que forma el segmento que une los dos centros, y los dos catetos serán (r – s) y x, así que se da la relación (r + s)² = x² + (r – s)², con lo que 2rs = x² – 2rs, así que x² = 4rs = 2s (recordemos que r = ½).
Por otra parte, la misma relación aparece como tangente entre la circunferencia contenedora y la de radio s, de forma que aquí, el segmento que une los dos centros será 1 – s (la circunferencia inicial es de radio 1, si usas otro hay que cambiar esto), y la relación es (1 – s)² = x² + s², por lo que 1 – 2s = x².
Uniendo ambas cosas, tenemos que 1 – x² = x², por lo que 2x² = 1, y así x = 1/raíz(2). Y s = x²/2 = ¼.
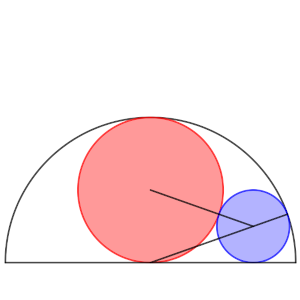
Ahora vamos a actuar de forma similar con la tercera circunferencia. Por un lado, es tangente a la circunferencia azul (cuyo centro era (1/raíz(2), ¼)), y el segmento que los une mide ¼ + t. Suponemos que sus coordenadas son (y, t), ya que la coordenada vertical debe coincidir con el radio para que sea tangente, y tenemos que (¼ + t)² = (¼ – t)² + (y – 1/raíz(2))².
Quitando paréntesis, tenemos que 1/16 + t/2 + t² = 1/16 – t/2 + t² + y² – 2y/raíz(2) +1/2. Si eliminamos los términos iguales, esta relación es equivalente a t – ½ = y² – 2y/raíz(2).
La otra relación de tangencia se comporta de manera similar a la de la segunda circunferencia, 1 – t es la longitud de la línea que une los centros, así que (1 – t)² = y² + t², por lo que 1 – 2t = y².
Uniendo ambas ecuaciones, tenemos que t = y² – 2y/raíz(2) + ½, por lo que 1 – 2t = 1 – 2y² + 4y/raíz(2) – 1 = y², es decir, que 4y/raíz(2) – 3y² = 0. como conclusión, ya que y no vale 0, es que y = 4/(3raíz(2)).
Como lo que nos piden es t, resulta que 1 – 2t = 16/18, por lo que 1 – 16/18 = 2t, y entonces t = 1/18.
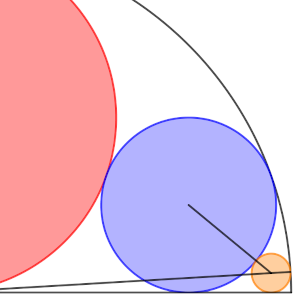
Puesto que hemos iniciado todo con el supuesto de que R = 1, hay que responder que k vale ¼ y h vale 1/18.
Ahora, que sabemos lo que da, para rehacer el trabajo sin que salgan (muchas) fracciones, podríamos haber empezado con un radio 36 = 9·4, que es múltiplo de ambos radios. Con eso, probablemente quedaría más limpio.