Problema 10 del concurso Olitele 2021 Se dirige a una edad de: 16-17 años
Queremos analizar qué estructuras geométricas puede tener un conjunto de puntos del plano con la propiedad de que si calculamos todas las distancias entre cualquier par de puntos del conjunto sólo resulten dos valores.
a) Comencemos por los conjuntos de tres puntos. Si están alineados, razona que el conjunto formado por dos extremos de un segmento y su punto medio cumple la propiedad pedida y ningún otro tipo de conjunto la tiene.
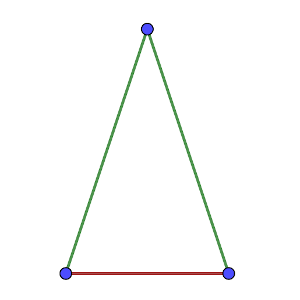
b) Pensemos ahora en los vértices de un triángulo. Si tomamos tres puntos que sean los vértices de un triángulo equilátero, este conjunto no cumple esa propiedad, ya que sólo aparece una única distancia entre todos ellos. Razona si existe o no un triángulo cuyos vértices formen un conjunto con esta propiedad.
c) Estudia qué estructuras pueden tener los conjuntos de 4 puntos del plano que cumplan la propiedad. Trata de indicar un camino para encontrarlas, dibújalas y justifica que cumplen la propiedad.
d) Repite el apartado anterior para conjuntos de 5 puntos.
Solución:
a) Supongamos que los tres puntos están alineados. Puesto que se trata de tres puntos, y deben de tener dos distancias entre ellos, el número total de distancias posibles entre ellos es tres AB, AC y BC, debe existir una de las tres distancias repetidas, y en todos los casos esas dos distancias tendrán un punto en común. Eso quiere decir que existe un punto a la misma distancia de otros dos.
Sobre una recta, el punto que está más a la derecha siempre está a dos distancias diferentes de los otros dos, si son diferentes, y lo mismo sucede con el que esté más a la izquierda, de forma que el que está comprendido entre los otros dos debe estar en el centro, para que esté equidistante a ambos.
Por lo tanto, los extremos de un segmento y su punto medio es el único conjunto de tres puntos alineados que cumple la condición.
b) Por la misma observación que hicimos en el primer párrafo del apartado (a), un punto debe estar exactamente a la misma distancia de los otros dos, y la distancia entre los otros dos debe ser diferente, por lo que el triángulo debe ser isósceles, no equilátero (según la definición, el triángulo equilátero podría ser considerado un tipo especial de triángulo isósceles).
De alguna forma, los tres puntos alineados podemos considerar que también formaban un triángulo isósceles de área cero.
c) Con cuatro puntos la clasificación es más diversa, ya que un subconjunto de 3 tendrán entre ellos, bien dos distancias, bien una única distancia.
Supongamos que tenemos tres puntos que sólo tienen una única distancia entre ellos. Está claro que no podemos añadir un cuarto punto que esté a la misma distancia de todos ellos en el plano, porque pertenecería simultáneamente a las tres circunferencias que podemos tazar con centro los tres vértices y radios las distancias.
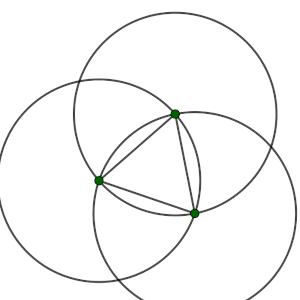
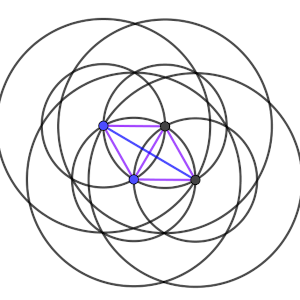
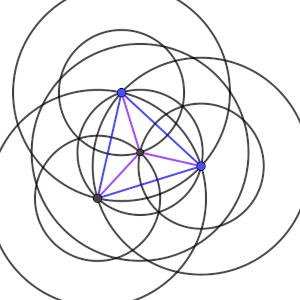
Una de las formas que podemos añadir un cuarto punto a la colección de tres es de forma que dos de las distancias sean la que ya existe entre ellos y establezca una distancia nueva con el otro, así que el cuarto punto debe estar en la intersección de dos de las circunferencias. A esta configuración le pondremos el nombre de C1.
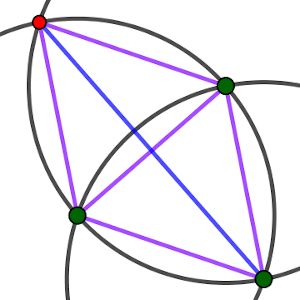
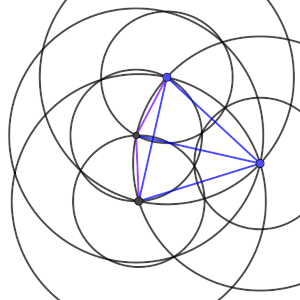
Ahora, otra de las formas que podemos añadir un nuevo punto de forma que aparezca una única segunda distancia es que sea equidistante con dos de los puntos del triángulo, y sobre la circunferencia centrada en uno de ellos, es decir, en la intersección de la circunferencia con la mediatriz de un segmento. Como la intersección sucede en dos puntos, diferenciaremos entre la configuración C2 y C3.
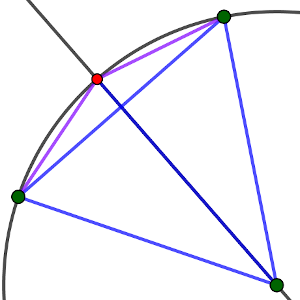
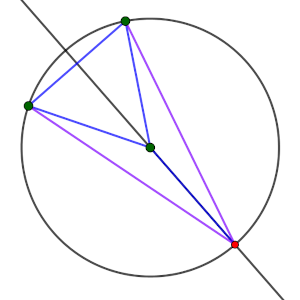
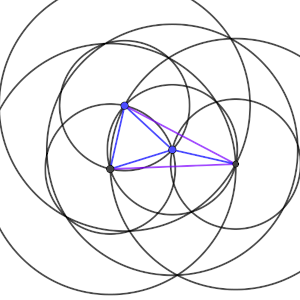
Por último, partiendo de esta configuración, podemos encontrar un punto que equidiste de los tres, observando el circuncentro del triángulo, lugar donde intersecan las tres mediatrices (C4).
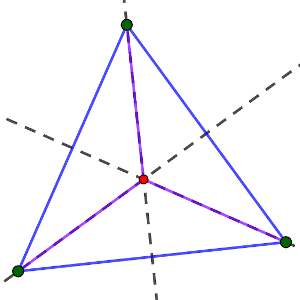
Veamos ahora os casos en que ninguno de los grupos de tres puntos pueda formar un triángulo equilátero. En ese caso, veamos qué combinación de distancias hay entre los cuatro puntos.
Supongamos que A está a la misma distancia x de B, C y D. Si eso es así, tenemos que entre ellos, ninguno está a la misma distancia x entre ellos, ya que si por ejemplo B y D estuviesen a la misma distancia x, entonces A, B y D formarían un triángulo equilátero. Pero eso significa que B, C y D están a distancia y entre ellos, con lo que forman un triángulo equilátero.
Por lo tanto, la única posibilidad es que A esté a distancia x de B y C, y a distancia y de D. Pero entonces, la distancia entre B y C debe ser también y para que no formen triángulo equilátero con A.
En estas circunstancias, se dan dos casos diferentes.
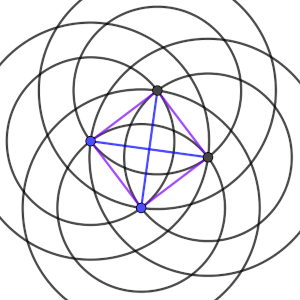
Si la distancia entre D y B y entre D y C son iguales a x (no pueden ser iguales a y, por formar entonces un triángulo equilátero), tendríamos un rombo ABCD, pero con las dos diagonales iguales, es decir, un cuadrado (C5).
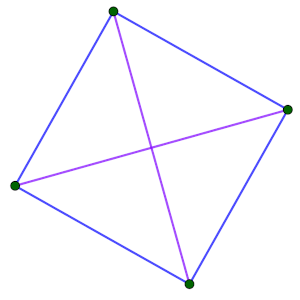
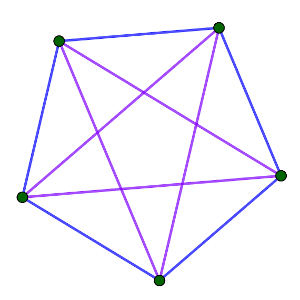
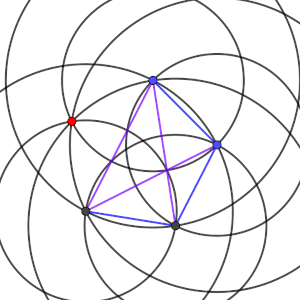
La última posibilidad es la más complicada de ver, y es que las distancias entre D y B y entre D y C sean diferentes, es decir, que una de ellas sea x y la otra y. Ambos casos son simétricos, supongamos que la distancia entre D y B sea x y que la distancia entre D y C sea y. En ese caso, tenemos un trapecio muy peculiar, con los triángulos CBD y DCA iguales, y también ABD y ABC. Si construimos un quinto punto E a la misma distancia x de C y D para formar un triángulo igual a ABC, podemos hacerlo de forma que la distancia entre E y B sea y por semejanza, y en ese caso tenemos un pentágono regular. Es decir, que nuestro trapecio en realidad estará formado por cuatro de los vértices de un pentágono regular (C6).
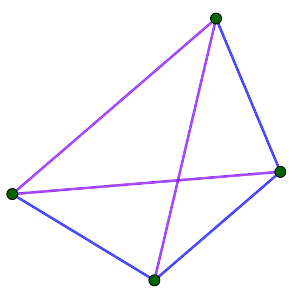
d) Continuar a partir de aquí puede parecer más complejo, pero en realidad está muy determinado. No puede haber un conjunto de 4 puntos del plano con la misma distancia entre ellos (en el espacio sí: los vértices de un tetraedro regular). Así que todo consiste en tomar las combinaciones de los cuatro puntos y comprobar si se puede o no añadir un quinto punto con la condición de que esté a una de las dos distancias con todos los demás. Su ubicación se puede obtener mediante construcciones con circunferencias (en cada punto dos centradas con las dos posibles distancias), y comprobar si está a la distancia debida o no (es decir, que en el mismo punto se cortan 4 circunferencias).
En C1, C2, C3, C4 y C5 es imposible, pero en C6 es lógico completarlo hasta el pentágono regular, con dos distancias entre todos ellos (el lado y la diagonal del pentágono regular).