Problema 12 del concurso Olitele 2021
Se dirige a una edad de: 16-17 años

Suma estas fracciones, obteniendo el resultado en forma de fracción irreducible:

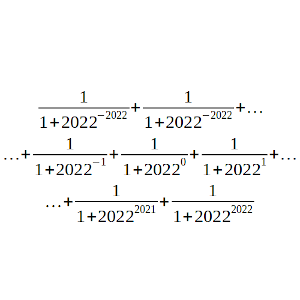
1/(1 + 2022^-2022) + 1/(1 + 2022^-2021)+ … + 1/(1 + 2022^-1) + 1/(1 + 2022⁰) + 1/(1 + 2022¹) + … + 1/(1 + 2022²⁰²¹) + 1/(1 + 2022²⁰²²)

Solución:

Es evidente que tenemos que hacer pruebas con números más bajos, como 1/(1 + 4^-4) + 1/(1 + 4^-3)+… 1/(1 + 4⁴) para ver qué sucede.

Y cuando manipulamos estas fracciones con sumas con exponentes negativos, lo que es evidente es que si queremos transformarlas de forma que no aparezcan estos exponentes, hay que multiplicar por la potencia adecuada.

Por ejemplo, 1/(1 + 4^-4) debemos multiplicarla por 4⁴ en su numerador y denominador para evitar que aparezcan potencias negativas, de forma que se transformaría en una fracción equivalente, 4⁴/(4⁴ + 1).
Y en ese momento nos podemos dar cuenta de que el denominador coincide con el de la fracción 1/(1 + 4⁴), que aparece en último lugar, por lo que podríamos sumar ambas fracciones sencillamente, obteniendo 4⁴/(4⁴ + 1) + 1/(1 + 4⁴) = (4⁴ + 1)/(1 + 4⁴) = 1.

Y si nos fijamos en las fracciones que tenemos que sumar en el enunciado, a ambos lados de la lista tenemos, en la posición 2021 – n, una fracciones de la forma 1/(1 + 2022^-n) = 2022ⁿ/(2022ⁿ + 1) a la izquierda y 1/(1 + 2022ⁿ) en la derecha, que sumadas dan (2022ⁿ + 1)/(1 + 2022ⁿ) = 1.

Sólo queda entonces un número que no es entero, el valor central, 1/(1 + 2022⁰) = 1/2. Contando la cantidad de términos que tiene la suma, tendremos que su valor es 2022 + 1/2 = 4045/2, que es la fracción buscada.