Problema 4 del concurso Marató de problemes 2022 Se dirige a una edad de: 14-15 años
Sabemos que se cumplen las igualdades siguientes:
A + B + C = m
C·B – A = n
A – C = p
Y que A, B y C son números naturales.
¿Cuál será el resultado de C·A + B (en función de m, n y p)?
(nota: a los participantes les daban valores concretos de m, n y p)
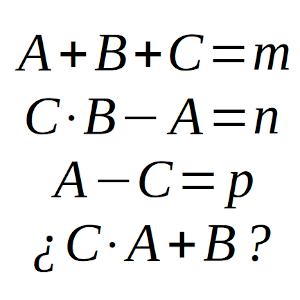
Solución:
Se trata de un sistema no lineal, y además hay muchas incógnitas.
Los primeros intentos deben ir encaminados no a resolver totalmente el sistema, si no a modificar las expresiones para obtener el valor objetivo. Si eso fracasa, ya tendremos tiempo de tratar de resolver.
Así, vemos que en realidad la ecuación más sencilla es la que nos dice que A = C + p, lo que nos permite transformar las demás, y también el objetivo.
B + 2C = m – p
C·B – C = n + p (también se puede expresar como C(B – 1) = n + p.
El objetivo pasa a ser C·C + p·C + B, es decir, C² + pC + B.
Ahora, la primera ecuación pasa a decirnos que B = m – p – 2C. Usando esa información, sustituimos en los demás y tenemos lo siguiente:
(m – p)C – 2C² – C = n + p, también se puede escribir como si fuese una ecuación de segundo grado, 2C² + (p – m + 1)C + n + p = 0
Y nuestro objetivo pasa a ser C² + pC + m – p – 2C = C² + (p – 2)C + m – p
Me da la impresión de que no puedo transformar una en la otra, así que no me queda más remedio que resolver y buscar el valor de C.
Hay dos soluciones. Parece muy complicado, pero debemos tener en cuenta que a los concursantes se les proporciona unos valores m, n y p de referencia, y que al menos una de las dos soluciones debe ser natural.
La primera solución sería C = (m – p – 1 + raíz(p² + m² + 1 + 2p – 2m – 2pm – 8n – 8p))/4
y la segunda sería C = (m – p – 1 – raíz(p² + m² + 1 + 2p – 2m – 2pm – 8n – 8p))/4.
A partir de ahí se sustituye en el objetivo.
Puede que en principio parezca dar dos soluciones, pero hay que tener cuidado y en ese caso calcular A y B, porque si una de ellas no da entera y positiva, esa solución queda descartada.
A lo largo del proceso he metido la pata varias veces, y ha sido de mucha utilidad darle valores concretos a A, B y C, y sustituir en los pasos intermedios. Si no daba lo mismo, lo revisaba detalladamente.
Por ejemplo, para A = 4, B = 2, C = 1, tenemos que m = 9, n = 2 y p = 1, con lo que al final obtenemos como primera solución C = (7 + raíz(25))/4 = 3 y como segunda C = (7 – raíz(25))/4, que no es entero. Evidentemente, el número que buscamos es 14 (sustituimos en C² – C + 8).
En otra ocasión, ambas soluciones han salido enteras y positivas (para m = 15, n = 32 y p = -4, las dos soluciones son 7 y 2), pero una de las dos ocasiona un valor negativo para la A, así que esa no es válida.