Problema 5 del concurso Marató de problemes 2022 Se dirige a una edad de: 14-15 años
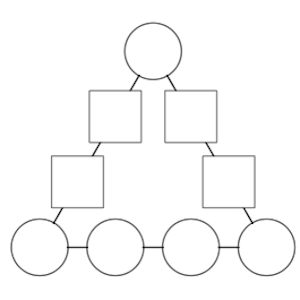
Queremos poner los números 6, 7, 8, 9, 10, 11, 12, 13 y 14 cada uno en un círculo o un cuadrado en la figura de la imagen, de forma que los números pares vayan en los círculos y los impares en los cuadrados, y que la suma de los número alineados en los tres lados del triángulo sea la misma para los tres lados.
¿Qué valor o valores puede tener esta suma?
En cada caso ¿qué número o qué números hay que poner en el círculo superior?
Solución:
Está claro que la suma de los tres lados es la de todos los pares menos uno.
La suma oscilaría entre 36 y 44.
Los cuatro impares, por su parte, aportan en los otros dos lados, y suman un total de 40, pero no pueden aportar lo mismo, ya que el número de arriba coincide, pero la de abajo no, y la suma debe coincidir. Según qué número agrupemos con el 7, dos pueden sumar 18 y los otros 22, o bien 16 y 24. En el primer caso, eso ocasiona una diferencia de 4 y en el otro 8.
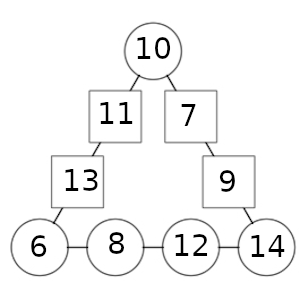
Para conseguir la diferencia de 8, tendríamos que poner los números extremos en los dos lados, el 14 y el 6. Eso ocasionaría una suma entre los impares y el par de bajo sumaría 30. A ambos habría que sumar el de arriba, teniendo en cuenta que tiene que dar lo mismo para 50 menos el de arriba que 30 más el de arriba, que no tiene más remedio que ser 40. Por eso, el de arriba sería el 10.
El reparto podría ser el siguiente:
Si la diferencia fuese 4, habría que poner una diferencia de 4 para compensar en los pares de abajo.
Si ponemos 6 y 10, eso ocasiona una suma (a falta de la cúspide) de 28, pero eso obligaría a que 28 + x = 50 – x, pero no puede ser impar (debería ser el 11).
Si ponemos 8 y 12, ocasiona una suma de 30, que ya vimos que se soluciona con una cúspide de 10.
Y por último, si fuese 10 y 14, sumaría 32, y tenemos que 32 + x = 50 – x, que de nuevo da impar (tendría que ser 9).
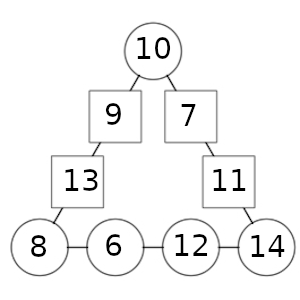
Así que, en cualquier caso, la suma es 30, y en el círculo superior hay un 10.