Problema 6 del concurso Marató de problemes 2022
Se dirige a una edad de: 14-15 años

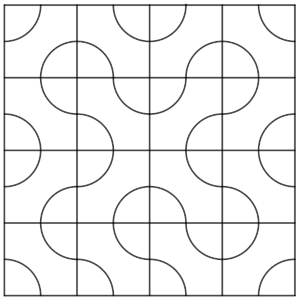
Disponemos de dieciséis baldosas cuadradas en las que aparecen dos cuartos de circunferencia centradas en esquinas opuestas cuyo radio es la mitad del lado de la baldosa.

Con ellas formamos un cuadrado, como en la imagen del ejemplo.

Veréis que en esta imagen hay una línea curva que conecta 12 de los arcos que hay, otra conecta 6 y otra conecta 5.

¿Cuál es el número máximo de arcos que podemos conectar en una curva cuando creamos el cuadrado de 16 baldosas?

Solución:

Es un ejercicio muy creativo, porque te permite hacer muchas composiciones.

Lo que está claro es que los arcos de los bordes tienen que tener una salida “hacia afuera” del cuadrado, de forma que de los 32 arcos, en cada lado hay que “descartar” el pase por 4 de ellos en cada lado, aunque podríamos hacer uno de entrada y otro de salida, de forma que de uno de los lados podemos utilizarlos para la curva.

Sin embargo, si situamos las baldosas de forma que un arco quede en las esquinas, éste arco se “cuenta” en dos lados, de forma que podemos ahorrar varios arcos, hasta contar sólo 12 en los bordes. Puesto que usamos dos para nuestra curva, perdemos sólo 2.

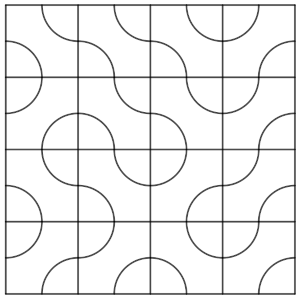
Puede que haya varias soluciones (me temo que no, salvo simetrías), pero el máximo de arcos de una curva será 32 – 10 = 22.

Un ejemplo lo tenemos a continuación: