Problema 13 del concurso Marató de problemes 2022
Se dirige a una edad de: 14-15 años

Tenemos 9 dados. Cuatro son de color ámbar, tres de color azul, y dos de color rojo.

Los dados de cada color son indistinguibles entre sí.

Los queremos poner, los nueve, unidos cada uno de ellos con el otro por un lado. En el dibujo aparece un ejemplo.

A) ¿De cuántas maneras podemos situar los dados, fijándonos únicamente en el color, de forma que cada uno de ellos tenga, tocándole, otro del mismo color?

B) ¿De cuántas formas podemos situar los dados para que ninguno de ellos tenga, tocándole, a ninguno del mismo color?

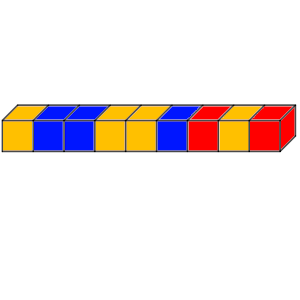
Solución:

La cantidad de posibilidades es muy grande, así que deberemos diseñar algún método para contarlos sin que se vuelva terriblemente largo.

A) El primer detalle es que los dos rojos deben aparecer juntos, con lo que eso nos evita muchas opciones. En segundo lugar, resulta que los tres de color azul deben también estar unidos, ya que al menos dos de ellos deben estarlo, y el tercero no puede situarse de forma independiente.

Por último, los cuatro ámbar deben estar, o bien los cuatro unidos, o bien en dos grupos de dos. A todos los efectos, consideraremos que están situados por parejas (pueden ser parejas unidas o separadas).

Una vez hechas estas observaciones, es fácil contabilizar que la cantidad de posiciones diferentes, entendiéndolas como posibles órdenes, sería permutaciones de los 4 bloques, pero divididas por 2, ya que los dos bloques del mismo color son intercambiables, es decir, 4·3·2/2 = 12.

Con letras, A ámbar, B azul y C rojo, tendríamos, citando las 12 situaciones:

AAAABBBCC
AAAACCBBB
AABBBAACC
AABBBCCAA
AACCAABBB
AACCBBBAA
BBBAAAACC
BBBAACCAA
BBBCCAAAA
CCAAAABBB
CCAABBBAA
CCBBBAAAA

B) La impresión que tenemos es que vamos a tener muchas más situaciones en las que no se toquen dos del mismo color. Sin embargo, vamos a diferenciar algunos casos especiales.

Si aparecen en los extremos dos de color no ámbar, nos quedan 7 posiciones para situar 4 ámbar, con lo que deberían estar alternados. En esos casos lo único que tenemos que decidir es de qué color entre azul y rojo, elegimos las cinco posiciones impares, y tenemos por tanto que elegir de las cinco posiciones, las dos en las que vamos a poner los rojos, quedando 20 posibles posiciones.

Supongamos que situamos un ámbar en un extremo, y uno no ámbar en el otro extremo. Nos quedan 7 posiciones para situar los 3 ámbar, pero no podemos poner uno junto al ámbar que tenemos en un extremo.

Para fijar ideas, supondremos que el primero es ámbar y el último el que no es ámbar. El segundo no puede ser ámbar, por lo que tenemos 6 posiciones posibles para los tres ámbar sin que toquen otro ámbar. Los podemos poner en posición par o en posición impar, pero habrá que tener cuidado con no poner del mismo color los dos no ámbar que van juntos.
De esta forma, tenemos los siguientes casos:

ABABABCAC
ABABACABC
ABABACACB
ABABACBAC
ABABCBABC
ABACABABC
ABACABACB
ABACABCAB
ABACACBAB
ABACBABAC
ABACBACAB
ABCABABAC
ABCABACAB
ABCACABAB
ACABABABC
ACABABACB
ACABABCAB
ACABACBAB
ACABCABAB
ACACBABAB

Un total de 20 posiciones posibles.

A estas 20 posiciones, hemos de añadir otras 20 en las que el ámbar del extremo está al final en lugar de al principio.

Por tanto, hemos contabilizado 20 + 20 + 20 = 60 posiciones.

Nos enfrentamos ahora al último subapartado, aquel en el que los dos extremos son ámbar. Nos quedan 7 posiciones para ubicar los demás, y tenemos que poner 3 azules, dos ámbar y dos rojos. Son muchos casos, pero podemos optar por subdividir a su vez este proceso según el número de azules que haya en primera y séptima posición, o hacer un conteo manual.

Con esta última opción, tenemos:

ABABACBCA
ABABCABCA
ABABCACBA
ABABCBACA
ABACABCBA
ABACBABCA
ABACBACBA
ABACBCABA
ABCABABCA
ABCABACBA
ABCABCABA
ABCACBABA
ABCBABACA
ABCBACABA
ACABABCBA
ACABCBABA
ACBABABCA
ACBABACBA
ACBABCABA
ACBACBABA
ACBCABABA

En total tengo 21 casos. Para enumerarlos, intento completar la primera combinación en orden alfabético en la que no hay dos letras repetidas, primera y última son A, y usa exactamente 4 A, 3 B y 2 C, y voy aumentando siempre la última letra posible, volviendo a situar las demás en orden correcto, y eliminando las que no sirven.
En total, habrá 21 + 20 + 20 + 20 = 81 posibles casos.