Problema 3 del nivel A de la Olimpiada Autonómica de la Comunidad Valenciana Se dirige a una edad de: 12-13 años
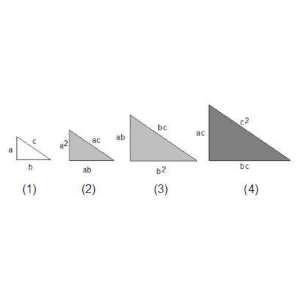
La siguiente imagen puede ser utilizada como una demostración del Teorema de Pitágoras.
Justifica matemáticamente esta demostración.
Solución:
No vi en un primer momento nada obvia la demostración, pero sí que es cierto que aparecen los tres lados del triángulo rectángulo al cuadrado.
Los cuatro triángulos son semejantes, ya que todos ellos guardan una proporción con él.
(2) Es un triángulo que está construido a escala a respecto al (1) original, (3) está construido a escala b y (4) está construido a escala c.
Eso quiere decir que los tres tienen exactamente los mismos ángulos, y, puesto que el ángulo entre los catetos, los lados de longitud a y b, es de 90º, eso significa que los otros dos ángulos agudos suman 90º.
Si giramos (3) en el espacio de forma que la hipotenusa esté en su base, coincide con uno de los catetos de (4), así que podemos situarlo sobre esta hipotenusa de forma que b² quede sobre la hipotenusa de 4, y el ángulo entre bc y ab una el ángulo recto de (4) y la hipotenusa.

Ahora, si tomamos (2) y hacemos un giro similar, de forma que la hipotenusa quede vertical, podemos situarlo también sobre el triángulo (4), de forma que la hipotenusa quede sobre el cateto vertical, y el lado que mide a² sobre la hipotenusa de (4).
Puesto que los ángulos agudos que están juntos de los triángulos (2) y (3) situados sobre (4) suman 90º, sus lados que están sobre la hipotenusa coinciden totalmente con la hipotenusa, probando con precisión que c² = a² + b².