Problema 3 de la Fase Local de la Olimpiada Española de Matemáticas 2023 (viernes mañana) Se dirige a una edad de: 16-17 años
Decimos que una terna (a, b, c) de números reales todos distintos de cero, es local, si:
a² + a = b²
b² + b = c²
c² + c = a².
(a) Probar que, si (a, b, c) es local, entonces (a – b)(b – c)(c – a) = 1.
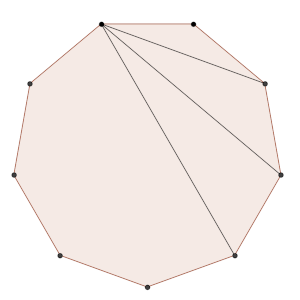
(b) Sea A₁ A₂ … A₉ un eneágono regular (polígono regular de 9 lados). Supongamos que |A₁A₄| = 1 y sea |A₁A₂| = a, |A₁A₃| = b y |A₁A₅| = c. Prueba que (a, b, -c) es local.
Solución: Aquí.