Problema 3 de la Fase Local de la Olimpiada Española de Matemáticas 2023 (viernes mañana) Se dirige a una edad de: 16-17 años
Decimos que una terna (a, b, c) de números reales todos distintos de cero, es local, si:
a² + a = b²
b² + b = c²
c² + c = a².
(a) Probar que, si (a, b, c) es local, entonces (a – b)(b – c)(c – a) = 1.
(b) Sea A₁ A₂ … A₉ un eneágono regular (polígono regular de 9 lados). Supongamos que |A₁A₄| = 1 y sea |A₁A₂| = a, |A₁A₃| = b y |A₁A₅| = c. Prueba que (a, b, -c) es local.
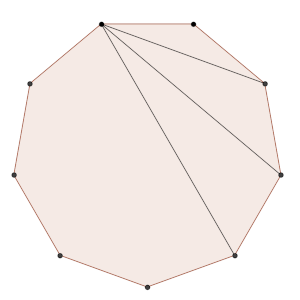
Solución:
Puesto que queremos mantener una cierta simetría con las tres letras, debemos tener en cuenta que al ser locales, una terna debe cumplir las tres condiciones, pero podemos expresarlas como una diferencia de cuadrados.
b² – a² = a
c² – b² = b
a² – c² = c
Por tanto, tenemos que b – a = a/(b + a), y de manera similar, c – b = b/(c + b) y también a – c = c/(a + c). Observamos que, puesto que ninguno de los tres números vale 0 y es producto de dos números, ninguno de los factores implicados puede ser 0.
Pero, además, si sumamos las tres igualdades, tenemos que 0 = a + b + c, es decir, que a + b = – c, b + c = a y (a + c) = – b.
Por lo tanto, b – a = – a/c, es decir, a – b = a/c, y de manera análoga, b – c = b/a y también c – a = c/b.
De esta forma, está claro que (b – a)(b – c)(c – a) = abc/(cab) = 1, ya que no pueden valer 0.
Ahora, para trabajar con un eneágono, debemos recurrir a utilizar el ángulo central y trigonometría no elemental, o bien el Teorema de Ptolomeo, que es equivalente, y estudiar cuidadosamente las relaciones entre las diferentes diagonales que aparecen.
Ahora bien, razonando sólo con triángulos semejantes es posible conseguirlo. Si construimos un cuadrilátero con las diagonales que constituyen a, b y 1 según el enunciado, tenemos la siguiente figura:
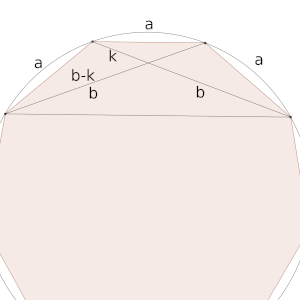
Dada la regularidad del eneágono, tenemos que cada una de las diagonales que miden b se cortan en segmentos que miden k y b – k. Además, por estar inscritos en una circunferencia, el ángulo que forma la diagonal b con la que mide 1 es el mismo que el que forma con el que mide a, por lo que el triángulo que se forma con las medidas b – k, a y k (en orden decreciente) es semejante al que forma 1, b y a. Eso quiere decir, por un lado que a/k = b/a, es decir, que k = a²/b, y 1/(b – k) = a/k, con lo que k = ab – a k, es decir, k + ak = ab, por lo que k = ab/(1 + a). De estas dos maneras diferentes de calcular k, deducimos que a²/b = ab/(1 + a), por lo que a/b = b/(1 + a), y por tanto a² + a = b².
Ahora, si buscamos la relación entre a y c, construimos otro cuadrilátero que contenga a y c, que podría ser el siguiente:
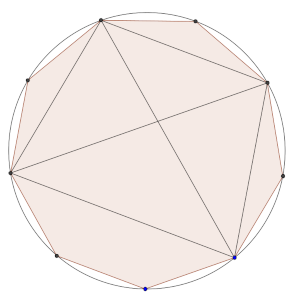
En este cuadrilátero de nuevo volvemos a encontrar el lado que mide c partido por otro lado que mide c, con lo que hay un triángulo formado por k, c – k y b que es semejante a otro formado por b, 1 y c, por lo que 1/(c – k) = c/b, y también b/k = c/b, de donde es sencillo deducir que b² + b = c². Es decir, que b² + b = (-c)².
Por último, los lados más difíciles de relacionar son a y c. Se puede recurrir a este cuadrilátero, pero debemos usar un ángulo determinado para cortar el segmento que hace de diagonal del cuadrilátero.
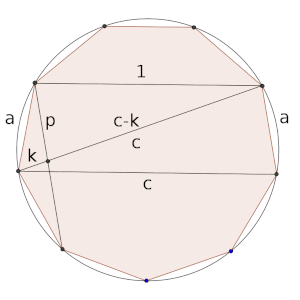
De esta forma, el triángulo formado por los segmentos que en el dibujo miden a, k y p, razonando por arcos inscritos, es decir, por el tamaño del arco que capturan, es semejante al que forman los segmentos que miden c, a y 1, por lo que se cumple que a/k = c/a. Por otra parte, el triángulo que forman los segmentos c – k, p y 1 es semejante al que forman c, a, y c (la diagonal). Esta proporción lo que nos dice es que es un triángulo isósceles, es decir, que 1 = c – k.
La primera relación nos dice que k = a²/c, mientras que la segunda nos dice que k = c – 1.
Uniendo ambas, tenemos que c – 1= a²/c, por lo que c² – c = a², o lo que es lo mismo, (-c)² + (- c) = a², que es lo que falta para probar que (a, b y -c) es una terna local.