Problema 6 de la Fase Local de la Olimpiada Española de Matemáticas 2023 (viernes mañana) Se dirige a una edad de: 16-17 años
Encontrar todos los enteros positivos a, b, c >= 1 que satisfacen la igualdad:
2^a + 7^b = c² + 4
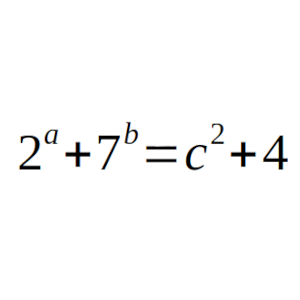
Solucion:
Es fácil ver que la igualdad se cumple si a vale exactamente 2, y b es un número par, con lo que c es el cuadrado de 7 elevado a la mitad de b.
Lo que es más difícil de probar es que no hay más soluciones. Si reescribimos la ecuación como 7^b = c² + 4 – 2^a, y trabajamos mediante restos al dividir por 8, tenemos dos casos.
Supongamos que a es 2. En ese caso, c² es una potencia de 7, y sólo puede ser c entero si b es par.
Supongamos que a vale 1. En ese caso, sea cual sea el valor de b, puesto que 7 = 8 – 1, tenemos que 7 elevado a cualquier potencia es necesariamente de la forma 8k + 1 o bien 8k – 1, según que sea b par o impar. Sin embargo, los cuadrados tienen, respecto al módulo 8, las siguientes configuraciones: 8k (si el número c es múltiplo de 4), 8k + 1 (si el número es de la forma 4k + 1 o 4k – 1), 8k + 4 (si c es de la forma 4k + 2). Por tanto, al sumarles 2, no pueden nunca coincidir.
Y si a es estrictamente mayor que 2, tenemos que 2^a es múltiplo de 8, por lo que 4 – 2^a es de la forma 8k + 4. De nuevo, tendremos que 7^b es de la forma 8k + 1 o bien de la forma 8k – 1, y c², por ser un cuadrado de un entero, sólo puede ser 8k, 8k + 1 o bien 8k + 4, con lo que al sumarle 8k + 4, pasa a ser de la forma 8k + 4, 8k – 3 o bien 8k, ninguna de las cuales puede coincidir con una potencia de 7.