Problema 8 de la Fase Local de la Olimpiada Española de Matemáticas 2023 (sábado) Se dirige a una edad de: 16-17 años
Encuentra todas las funciones reales de variable real que cumplen que f(x + f(y + f(x + f(y + f(x))))) = 3x + 2y para cualesquiera x, y.
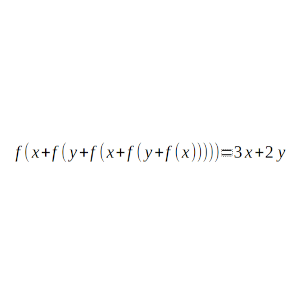
Solución:
Todas las ecuaciones funcionales son problemas que se resuelven dando inicialmente valores concretos para pasar a generalizar según vamos alterando parámetros.
En este caso, puesto que la ecuación tiene sumas, vamos a considerar el caso x = 0, y también y = 0.
Puesto que f(0 + f(0 + f(0 + f(0 + f(0))))) = 0, sabemos que existe un valor, c tal que f(c) = 0. Concretamente, f(c + f(c + f(c + f(c + f(c)))) = 5c, pero como f(c) = 0, tenemos que si vamos sustituyendo, 0 = 5c, por lo que c = 0.
Al menos tenemos un valor, ahora veamos qué sucede con un valor cualquiera a. Supongamos que conocemos f(a), y si hacemos y = -f(a), tendremos que y + f(a) = 0, así que sustituyendo en la fórmula x por a y el valor y por -f(a), tendremos que f(a + f(-f(a) + f(a + f(-f(a) + f(a))))) = f(a + f(-f(a) + f(0))) = f(a + f(0)) = f(a), pero por otra parte, es igual a 3a – 2f(a), por lo que 3f(a) = 3a, y por tanto f(a) = a.
Es decir, que la única función que puede que cumpla la condición es f(x) = x. Es sencillo ver que, en efecto, la cumple.