Problema 4 del nivel B de la Fase Comarcal de la Olimpiada de la Comunidad Valenciana
Se dirige a una edad de: 14-15 años

Decimos que un número que tiene un número par de cifras es un número doble si la primera mitad de las cifras forma un número que es el doble del número que forma la segunda mitad de sus cifras.

Así los números 84 y 2010 son números dobles porque 8 = 2·4 y 20 = 2·10 respectivamente.

¿Cuántos números dobles hay entre 0 y 10000?

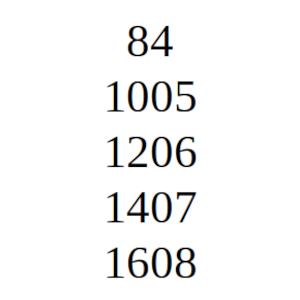
Solución:

Creo que este era el problema más sencillo, siempre que nos diésemos cuenta de los detalles.

Debemos usar sólo números con una cantidad par de cifras, de 2 cifras y de 4 cifras.

Eso quiere decir que la segunda mitad de sus cifras, en el caso de ser números de 2 cifras, sólo puede ir de 1 a 4, ya que estamos limitados a aquellos números cuyo doble tiene 1 cifra, y los de cuatro cifras, podemos usar desde 05 hasta 49, ya que números mayores deberían tener más de 2 cifras en su doble.

De esta forma, tendremos 49 números dobles en total.

Puede que no podamos admitir en sentido estricto los números de cuatro cifras en la que los dos finales empiezan con 0, y en ese caso deberíamos eliminar de la cuenta los 5 números 1005, 1206, 1407, 1608 y 1809, aunque en mi opinión también deben ser considerados números dobles.