Problema 1 de la Fase Local de la Olimpiada Española de Matemáticas 2024 (viernes) Se dirige a una edad de: 16-17 años
Hallar el menor entero positivo n tal que la suma de n sumandos
A(n) = 1 + 11 + 111 + … + 11…1
es divisible por 45.
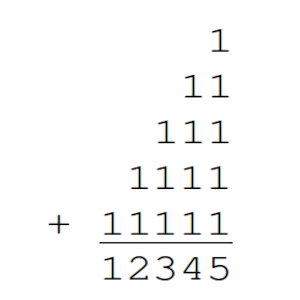
Solución:
Este problema se puede solucionar sin tener muchos conocimientos, pero podría convenir saber cosas de divisibilidad a la hora de buscar patrones, ya que a partir de cierto punto las sumas directas se pueden volver muy largas y las posibilidades de equivocarse están muy presentes.
Es sencillo sumar los primeros y probar a dividir, con lo que rápidamente vemos un patrón en las cifras del resultado. Puesto que los primeros no son claramente divisibles por 45, podemos llegar a la décima suma con facilidad, donde veremos que se rompe el patrón de las cifras por culpa de exceder de 10 algunos valores y empiezan a complicarse las cosas.
Claro, que viendo que 45 es el producto de 5 por 9, rápidamente entendemos que hay que estudiar la divisibilidad por 5 y la divisibilidad por 9, que son bastante conocidas.
Como la divisibilidad por 5 depende sólo de la última cifra, y el patrón de la última cifra de la suma va variando de 1 en 1, está claro que n debe ser múltiplo de 5, con lo que podemos fácilmente probar qué da en los casos de 5 y de 10, viendo que ninguno de los dos es divisible también por 9, así que deberíamos estudiar la divisibilidad por 9.
Aquí hay dos aproximaciones muy diferentes. Si nos centramos en restos módulo 9, (es decir, el resto a dividir entre 9, o qué diferencia hay entre un número y el mayor múltiplo de 9 menor que ese número), es fácil estudiar el resto de los números de la sucesión 1, 11, 111, …
Voy a utilizar el símbolo ≡ para referirme a partir de ahora a equivalente módulo 9
1 ≡ 1
11 ≡ 2
111 ≡ 3
1 111 ≡ 4
Sucesivamente, llegamos que el término 9 es
111 111 111 ≡ 0 (es múltiplo de 9)
Y a partir de ahí, volvemos a empezar, es decir, se produce un ciclo de 9 posibles restos y volvemos a empezar.
Pero nuestro objetivo son las sumas, así que empezamos de nuevo
n = 1, 1 ≡ 1
n = 2, 12 ≡ 1 + 2 = 3
n = 3, 123 ≡ 3 + 3 = 6
n = 4, 1234 ≡ 6 + 4 = 10 ≡ 1 (observa que los restos se pueden sumar tranquilamente, ya que la parte divisible por 9 al sumarse sigue siendo divisible por 9)
n = 5, 12345 ≡ 1 + 5 = 6
n = 6, 123456 ≡ 6 + 6 = 12 ≡ 3
n = 7, 1234567 ≡ 3 + 7 = 10 ≡ 1
n = 8, 12345678 ≡ 1 + 8 = 9 ≡ 0 (múltiplo de 9)
n = 9, 123456789 ≡ 0 + 0 = 0 (múltiplo de 9)
n = 10, 1234567900 ≡ 0 + 1 = 1 ¡Vuelve a comenzar! Esto sucede porque volvemos a sumar la misma secuencia a cero.
Eso quiere decir que en la sucesión A(n) hay una secuencia de restos al dividir por 9 en la que 7 números no lo son y dos sí.
Ahora, si nos preguntamos dónde están los primeros restos si avanzamos de 5 en 5 por esa secuencia, veremos lo siguiente:
1 (n = 10)
3 (n = 20)
6 (n = 30)
1 (n = 40)
6 (n = 5)
3 (n = 15)
1 (n = 25)
0 (n = 35)
0 (n = 45)
Por lo que está claro que el primer valor para el que es divisible por 5 y por 9 sería 35, y 45 sería el segundo.
Otra aproximación más rápida e ingeniosa, significa quedarnos con algo diferente del patrón que hemos visto:
1 ≡ 1
11 ≡ 2
111 ≡ 3
1 111 ≡ 4
Sucesivamente, llegamos que el término n tiene el mismo resto que n
Y claramente por tanto las sumas van a tener el mismo resto que 1 + 2 + … + n, que si sabemos sumar progresiones aritméticas (ésta es la que ponen siempre de ejemplo como la anécdota de Gauss) da lo mismo que (n + 1)·n/2, y claramente sólo dará múltiplo de 9 bien si n es múltiplo de 9 o bien si n + 1 lo es.
Probando los diferentes múltiplos de 5, vemos que:
ni 5 ni 6 son múltiplo de 9
10 y 19 tampoco
15 y 16 tampoco
Y así sucesivamente hasta 35, que sí va a producir un A(35) múltiplo por ser múltiplo 36 = 9·4.
El siguiente sería 45, evidentemente, y el siguiente ya sería 80.
como se puede apreciar, es un método mucho más rápido, pero no siempre es fácil de encontrar.
Las secuencias pueden volverse, en algunos casos, muy complejas. Por ejemplo, si estudiamos la divisibilidad por 7, el patrón de repeticiones parece muy caprichoso, ya que esconde una secuencia de longitud 49, en el que el patrón da divisibilidades intercaladas, hasta empezar a repetirse.
Pedir por ejemplo cuándo es divisible por 63 podría ponernos en serios aprietos.