Problema 7 de la Fase Local de la Olimpiada Española de Matemáticas 2024 (viernes)
Se dirige a una edad de: 16-17 años

Sea a > 1 un número real.

Encontrar todas las soluciones de la ecuación: raíz(a – raíz(a + x)) = x en función de a.

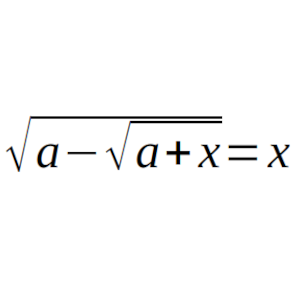
Solución:

Aunque se trata de una ecuación solamente, requiere un análisis relativamente difícil.

Evidentemente, debemos empezar por eliminar las raíces, de forma que tenemos que a – raíz(a + x) = x² para cierta x mayor que cero. Además, observa que x debe ser menor o igual que raíz de a.

Despejando de esta ecuación, tenemos que raíz(a + x) = a – x², por lo que a + x = a² – 2ax² + x⁴.

Esta relación es de cuarto grado en x, pero sólo de segundo grado en a, así que nos decantaremos por esa manera de establecer la relación entre a y x. De esta forma, tenemos que a² – a(2x² + 1) + x⁴ – x = 0. Por lo tanto, tenemos dos soluciones posibles para a.

La primera opción sería a = ((2x² + 1) + raíz( 4x⁴ + 4x² + 1 – 4x⁴ + 4x))/2 = ((2x² + 1) + raíz( 4x² + 1 + 4x))/2 = (2x² + 1 + 2x + 1)/2 = x² + x + 1. En este caso, tenemos que x = (-1 + raíz(4a – 3))/2. Es sencillo ver que esta solución sí que cumple el enunciado, mientras que la correspondiente solución con un signo negativo para la raíz da lugar a una x negativa, que no cumple la ecuación.

La segunda opción sería similar, pero con la raíz negativa, y en ese caso, a = x² + x, con lo que x = (1 + raíz(4a + 1))/2, ya que la otra solución es negativa, y de todas formas esta solución no es válida por ser x mayor que raíz(a), y entrar en conflicto con el segundo párrafo.

Ya que la única solución es que x = (-1 + raíz(4a – 3))/2, sólo puede darse si 4a – 3 es mayor o igual que 1, de forma que a debe ser mayor o igual que uno, como afirma el enunciado.