Problema 4 de la Fase Nacional de la de la LV OME 2019
Se dirige a una edad de: 16-17 años

Calcular todos los pares de enteros (x, y) que cumplen la siguiente igualdad: 3⁴·2³ (x² + y²) = x³·y³.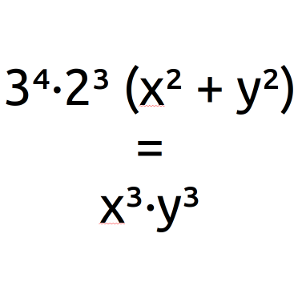
Solución:

En primer lugar, puesto que el primer término es claramente múltiplo de 3, el segundo también lo es, por lo que uno de los dos factores diferentes, x o y, es múltiplo de 3.

Pero el otro también debe serlo, porque en caso contrario, x² + y² no sería múltiplo de 3, y la cantidad de factores primos 3 que aparecerían en el producto no sería múltiplo de 3 (habría sólo 4), mientras que se trata de un producto de dos cubos, y todos los factores primos estarán en una cantidad múltiplo de 3.

Por lo tanto, x = 3a, e y = 3b, por lo que la expresión 3⁴·2³ (x² + y²) = 3⁴·2³ (9a² + 9b²) = 3⁶·2³ (a² + b²), y la expresión x³·y³ = 3⁶a³·b³.

Entonces la igualdad queda 2³(a² + b²) = a³·b³.

A partir de aquí, sabemos que al menos uno de los dos debe ser par, pero el razonamiento en términos de par o impar no es sencillo, aunque se puede hacer.

Puesto que el primer término es mayor o igual que 0, sabemos que a y b tienen que tener el mismo signo (ambos negativos, o ambos positivos). Un cambio de signo dará soluciones de otro signo, así que podemos suponer que ambos son positivos (o nulos), y deducir las soluciones con números negativos.

Puesto que ambos números juegan el mismo papel en la expresión, podemos suponer que a es mayor o igual que b, sin pérdida de generalidad, y en ese caso, 16a² >= 8(a² + b²) = a³·b³, es decir, 16a² >= a³·b³, y simplificando a² (si es distinto de 0), tenemos que 16 >= ab². Es decir, que los valores quedan acotados.

En caso de que b = 0, resulta que a = 0 y tenemos una solución (es muy sencillo ver que si uno de los dos es 0, ambos deben ser 0).

Si tenemos que b = 1, entonces 8(a² + 1) = a³, ecuación que no tiene ninguna solución entera positiva (sabemos que las soluciones deberían ser 1, 2, 4, 8, y no valen).

Si b = 2, tenemos que 8(a² + 4) = 8a³, es decir, a² + 4 = a³, que tiene sólo la solución a = 2.

Y si b es mayor que 2, ab² es mayor o igual que 27 (recuerda que a es mayor o igual que b), por lo que tampoco es posible.

Así, las soluciones son tres. La primera es que x = y = 0, la segunda, que x = y = 6 y la tercera, que x = y = -6.

Nuestro colaborador Javier Nistal nos envía una variante.

Una vez que llegamos a que 2³(a² + b²) = a³·b³, uno de los dos está claro que es par, ya que el producto es múltiplo de 2, y por simetría, podemos suponer que a = 2c, por lo que queda 4c² + b² = c³b³.

Si c = 0, entonces claramente b = 0. En caso contrario, tenemos que, dividiendo por c, 4 + (b/c)² = cb², por lo que claramente c divide a b.

Por tanto, b = ck, y como ambos tienen que tener el mismo signo, k > 0. Y 4 + k² = c⁴k³.

Y, por tanto, (2/k)² + 1 = c⁴k, por lo que k divide a 2. Así que es 1 o 2.

Si k = 1, queda 5 = c⁴, que no tiene solución.

Si k = 2, entonces 1 + 1 = 2c⁴, que sólo tiene soluciones c = 1 y c = -1.

Esos dos casos nos llevan a que a = b = 2 o bien a = b = -2, lo que a su vez implica que x = y = 6, o bien x = y = -6.

Por lo que tenemos las tres soluciones dichas anteriormente, (0, 0), (6, 6) y (-6, -6) únicamente.