Problema 2 de la Olitele 2019
Se dirige a una edad de: 16-17 años

¿Cuántos números de cuatro cifras (desde el 1000 hasta el 9999) hay que cumplan que la suma del número formado por las dos primeras cifras, más la cifra de las decenas, más la de las unidades, sea igual que el número formado por las dos últimas cifras?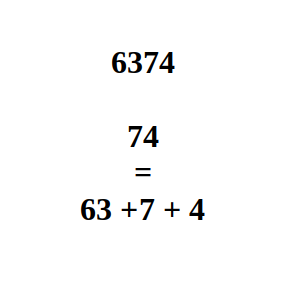
Solución:

Empleando un poco de álgebra, tenemos que el número se puede escribir como a·100 + b + c (a es el número de dos cifras que forman las dos primeras cifras, b las decenas y c las unidades).

Y el número que forman las dos últimas cifras es 10b + c, de forma que la condición es que 10b + c = a + b + c, por lo que la ćondición se entiende mejor como 9b = a, donde b es un número de una cifra y a es otro de dos cifras.

Claro que hay muchas posibilidades para esto, desde b = 2 hasta b = 9 tenemos 8 casos para valores concretos de a (valores de b menores no dan dos cifras para a), y esos 8 casos admiten cualquier cifra de las 10 posibles para c, así que tenemos 80 números de ese tipo.