Problema 2 de la Olitele 2019 Se dirige a una edad de: 16-17 años
¿Cuántos números de cuatro cifras (desde el 1000 hasta el 9999) hay que cumplan que la suma del número formado por las dos primeras cifras, más la cifra de las decenas, más la de las unidades, sea igual que el número formado por las dos últimas cifras? 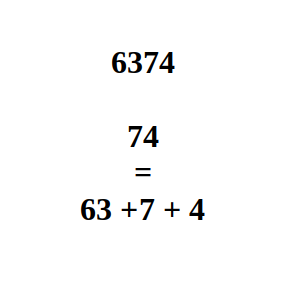
Solución: Aquí.
La solución es simple. Denotemos el número de 4 cifras como abcd (sólo como representación de las cifras del número, no como su multiplicación). Reescribamos este número algebraicamente como 1000a+100b+10c+d, visto así tras algo de álgebra, el enunciado puede verse como la siguiente ecuación: 10a + b + c + d = 10c + d; simplificando nos queda: 10a + b = 9c.
Sabemos que 0<= c <= 9 y que por lo tanto 10a + b <= 81. De ahí también obtenemos que 1<= b <= 9 (ya que ningún múltiplo de 9 termina en 0 podemos omitirlo del rango de "b"). Por último sabemos que 0<= a <= 8 (puesto que el máximo número que podemos alcanzar es 81 podemos omitir 9 del rango de "a").
Ahora, puesto que 10a + b = 9c sabemos que para cada valor de c va a haber una y sólo una posible configuración posible de a y b en concreto habrá 9 posibles configuraciones cada una de ellas para una de las soluciones de la tabla del 9.
Sin embargo no podemos olvidarnos de "d" puesto que aunque se haya cancelado algebraicamente, esta sigue siendo una de las cifras de nuestro número original. Como hemos visto, "d" se cancela, lo cual significa que no tiene ninguna relevancia en nuestra igualdad principal, justo por esta razón, podemos asignarle cualquier valor (siempre y cuando 0<= d <= 9) por lo tanto, el total de números de 4 cifras posibles que cumplan esta propiedad es 9 · 9 = 81.
Corrección: el número ha de ser 10 · 8 = 80, ya que como el número de cuatro cifras a de ser por lo menos el 1000, 1<= a <= 9 y por tanto
10 · 1 + b = 9 · 1 no tiene solución con 1<=b <= 9. Por otro lado, si consideramos 0<= d <= 9 vemos que en verdad desde 0 hasta 9 contamos 10 números. Por tanto la solución final es 8 · 10 = 80.