Problema 1 de la Fase Catalana de la OME 2019 Se dirige a una edad de: 16-17 años
Cinco puntos, P, P1, P2, P3 y P4, están sobre la misma circunferencia.
Demuestra que el producto de la distancia desde P a la recta P1P2 por la distancia desde P a la recta P3P4 es igual al producto de las distancia desde P a la recta P1P3 por la distancia desde P a la recta P2P4.
(En la imagen se puede acceder a un ejemplo interactivo, en el que se pueden mover los puntos)
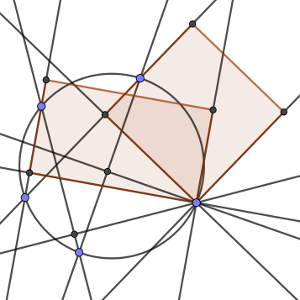
Solución:
Hay muchas aproximaciones a este problema.
Una de ellas consiste en parametrizar los cuatro puntos con expresiones trigonométricas, situando el eje de coordenadas sobre el centro de la circunferencia, de forma que el punto P, por ejemplo, esté situado en el punto de coordenadas (1,0). A partir de ahí, se trata de calcular el valor de estas dos distancias en función de los ángulos que se forman desde el centro por los otros cuatro puntos y comprobar que la expresión es realmente la misma. Sin embargo, las expresiones son lo suficientemente complejas para que cualquier error produjese una gran pérdida de tiempo.
La forma que más me gusta es trabajar sólo con tres puntos inicialmente, por ejemplo, P, A y B. Todos ellos están en una circunferencia, y se trata de escribir de otra forma la distancia de P a la recta AB. Por ejemplo, vemos que la distancia se puede calcular como PA*sin(PAB) o como PB*sin(PBA).
El hecho de que salga el seno en la fórmula, nos puede sugerir relacionarlo con el teorema del seno, y recordar de dónde podemos deducir la famosa igualdad (que en este caso diría que PA/sin(PBA) = PB/sin(PAB) = AB/sin(APB).
¿Por qué esto es así? Una demostración clásica dice, que puesto que estos tres puntos están en una circunferencia (todos los vértices de un triángulo lo están), el ángulo PAB, por ejemplo, siempre vale lo mismo, aunque el punto A se mueva por el arco de la circunferencia, de forma que podemos situarlo de forma que el lado PA pase por el centro, de forma que su medida será exactamente 2R (ya que será un diámetro). Pero, de esta forma, el seno será PB/2R, puesto que se tratará de un triángulo rectángulo. Luego PB/sin(PAB) = 2R. De forma análoga, se dan las otras igualdades. Lo importante es que todos estos cocientes valen lo mismo, 2R. De forma que sin(PAB) lo podemos calcular como PB/2R. En un triángulo genérico, este valor de R dependería del triángulo, pero en este caso, todos los triángulos están sobre la misma circunferencia.
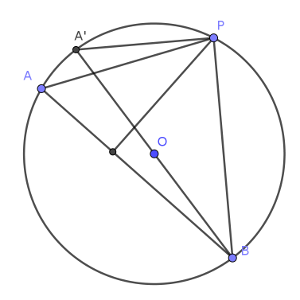
En el caso en que P y B estén en el mismo lado que A del diámetro, la igualdad se da también, aunque no es tan evidente.
En nuestro caso, eso significa que la distancia de P a la recta AB se puede escribir como PA·sin(PAB) = PA·PB/(2R).
En el contexto del problema, el producto de la distancia desde P a la recta P1P2 por la distancia desde P a la recta P3P4 se podría escribir entonces como (PP1·PP2/(2R))·(PP3·PP4/(2R)) = (PP1·PP2·PP3·PP4)/(4R²), ya que ambos triángulos están sobre la misma circunferencia.
Y, claro, la distancia desde P a la recta P1P3 por la distancia desde P a la recta P2P4 nos proporciona el mismo resultado, (PP1·PP3/(2R))·(PP2·PP4/(2R)) = (PP1·PP2·PP3·PP4)/(4R²).