Problema 2 de la Olitele 2018 Se dirige a una edad de: 16-17 años
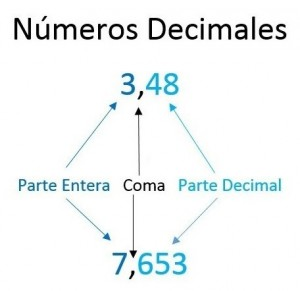
En este ejercicio, [x] representa la parte entera del número x, y {x}, su parte decimal.
¿Cuánto suman las soluciones de la ecuación 10[x] + 20{x} = K?
Solución: Aquí.
Problema 2 de la Olitele 2018 Se dirige a una edad de: 16-17 años
En este ejercicio, [x] representa la parte entera del número x, y {x}, su parte decimal.
¿Cuánto suman las soluciones de la ecuación 10[x] + 20{x} = K?

Solución: Aquí.
Problema 1 de la Olitele 2018 Se dirige a una edad de: 16-17 años
En una cuadrícula de puntos plana cuyos puntos distan un centímetro del más próximo horizontal y verticalmente, dibujamos un triángulo que se apoya en los puntos de coordenadas (0, 0), (4, 3) y (1, 4), y un cuadrado en los vértices (1, 1), (2, 1), (2, 2) y (1, 2), como indica la figura.
¿Cuál es el área de la parte común?

Solución: Continue reading Solución a triángulo y cuadrado en una rejilla
Problema 1 de la Olitele 2018 Se dirige a una edad de: 16-17 años
En una cuadrícula de puntos plana cuyos puntos distan un centímetro del más próximo horizontal y verticalmente, dibujamos un triángulo que se apoya en los puntos de coordenadas (0, 0), (4, 3) y (1, 4), y un cuadrado en los vértices (1, 1), (2, 1), (2, 2) y (1, 2), como indica la figura.
¿Cuál es el área de la parte común?

Solución: Aquí.
Problema 0 de la Olitele 2018 Se dirige a una edad de: 16-17 años
¿Cuántas soluciones enteras tiene el sistema de ecuaciones x² = y³ = K para valores de k menores que 20182019?
Nota: una solución es una terna (x, y, k).
En este problema se piden los casos en los que tanto x, como y, como k, son números enteros.
Solución:
Continue reading Solución a menores que 20182019
Problema 0 de la Olitele 2018 Se dirige a una edad de: 16-17 años
¿Cuántas soluciones enteras tiene el sistema de ecuaciones x² = y³ = K para valores de k menores que 20182019?
Nota: una solución es una terna (x, y, k).
En este problema se piden los casos en los que tanto x, como y, como k, son números enteros.
Solución: Aquí.
Regalo estacional de los organizadores de la edición 2019 de la Olimpiada Internacional Se dirige a una edad de: 16-17 años
Una entrada es una cadena de ceros y unos.
A partir de ella, escribimos una fila de unos y ceros usando las reglas del triángulo de Pascal, donde cada uno de los números es suma de los dos situados en diagonal por encima suyo.
Trabajamos “módulo 2”, es decir, 1 + 1 = 0.
Repetimos el proceso hasta que formamos un triángulo de números.
Por ejemplo, si la entrada es 1 0 1 1 1, el triángulo sería el siguiente:
1 0 1 1 1
1 1 0 0
0 1 0
1 1
0
La salida de este procedimiento es la cadena de unos y ceros que se puede leer en el lado de este triángulo desde el extremo inferior hasta el extremo superior derecho, en ese orden. En nuestro ejemplo es 0 1 0 0 1.
Si decidimos empezar con una entrada de longitud n, hay 2n posibles cadenas de entrada.
¿Cuántas de esas cadenas tienen la propiedad de que son las mismas que su cadena de salida correspondiente?
No son necesarios cálculos complejos. Use sólo ideas hermosas.

Solución:
Continue reading Solución a triángulo de Pascal binario
Si te declaras culpable de derivadas e integrales, curvas y superficies, variables aleatorias y funciones de densidad, anillos, cuerpos y conmutatividades varias…
¡Customiza tu foto en Powerpoint con unas rejas sobre un fondo matemático!
Regalo estacional de los organizadores de la edición 2019 de la Olimpiada Internacional Se dirige a una edad de: 16-17 años
Una entrada es una cadena de ceros y unos.
A partir de ella, escribimos una fila de unos y ceros usando las reglas del triángulo de Pascal, donde cada uno de los números es suma de los dos situados en diagonal por encima suyo.
Trabajamos “módulo 2”, es decir, 1 + 1 = 0.
Repetimos el proceso hasta que formamos un triángulo de números.
Por ejemplo, si la entrada es 1 0 1 1 1, el triángulo sería el siguiente:
1 0 1 1 1
1 1 0 0
0 1 0
1 1
0
La salida de este procedimiento es la cadena de unos y ceros que se puede leer en el lado de este triángulo desde el extremo inferior hasta el extremo superior derecho, en ese orden. En nuestro ejemplo es 0 1 0 0 1.
Si decidimos empezar con una entrada de longitud n, hay 2^n posibles cadenas de entrada.
¿Cuántas de esas cadenas tienen la propiedad de que son las mismas que su cadena de salida correspondiente?
No son necesarios cálculos complejos. Use sólo ideas hermosas.

Problema 3 de la Olimpiada Matemática Femenina Europea (EGMO 2018) Se dirige a una edad de: 16-17 años
Las n concursantes de cierta EGMO se llaman C1, C2, … ,Cn. Después de la competencia, se ponen en fila fuera del restaurante de acuerdo a las siguientes reglas:
· El Jurado escoge el orden inicial de las concursantes en la fila.
· Cada minuto, el Jurado escoge un entero i, con 1 ≤ i ≤ n.
Si la concursante Ci tiene al menos otras i concursantes delante de ella, le paga un florín al Jurado y se mueve exactamente i posiciones delante de ella.
Si la concursante Ci tiene menos de i concursantes delante de ella, el restaurante se abre y el proceso termina.
(a) Demuestre que el proceso no puede continuar indefinidamente, sin importar las elecciones del Jurado.
(b) Determine para cada n el máximo número de florines que puede recolectar el Jurado, escogiendo el orden inicial y la secuencia de movimientos astutamente.
Solución: Continue reading Solución a una fila en Florencia