Problema 1 de la Fase Nacional de la Olimpiada Española de Matemáticas 2022 (viernes) Se dirige a una edad de: 16-17 años
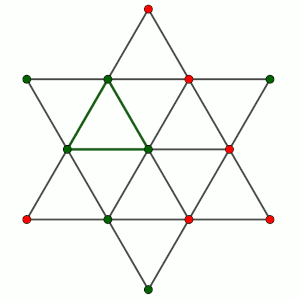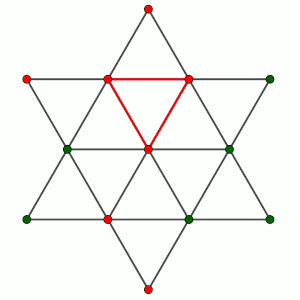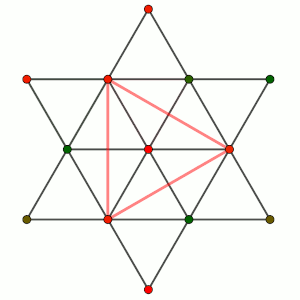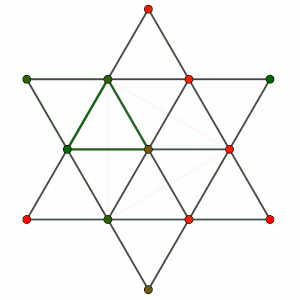
La estrella de seis puntas de la figura es regular: todos los ángulos interiores de los triángulos son iguales.
A cada uno de los trece puntos señalados se le asigna un color: verde o rojo.
Demuestra que siempre habrá tres puntos del mismo color que son vértices de un triángulo equilátero.
(No estaba en el enunciado, pero se entiende que el triángulo equilátero del que son vértices puede no estar trazado en las líneas de la figura dibujada.)
Solución:
La clave de este problema es tratar de razonar ordenadamente todos los casos. Suponer que existe una combinación de colores que no cumple el enunciado y llegar a una contradicción.
Hay varios razonamientos posibles, por ejemplo, empezando por el centro de la estrella, lo suponemos de uno de los dos colores (evidentemente, no se pierde generalidad, en caso de serlo del otro, bastaría invertir el razonamiento). Si hay en los 6 puntos que forman el hexágono que rodea a este punto central dos vértices consecutivos de ese mismo color, evidentemente forman un triángulo equilátero con el central.
Por tanto, no puede ser que los 6 puntos sean del mismo color que el centro.
Tampoco pueden ser 5 de ellos ni 4 del mismo color que el centro, puesto que necesariamente habría dos puntos consecutivos.
Si fuesen 3 del mismo color que el centro, los otros 3 deberían ser del otro, y estarían colocados alternativamente para evitar que hubiese dos consecutivos, pero uniendo tres puntos de uno u otro color se formaría un triángulo equilátero con tres vértices del mismo color.
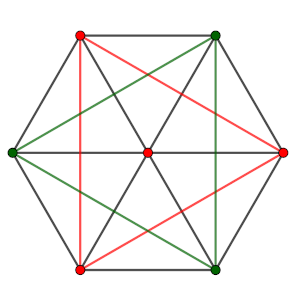
Tampoco puede ser sólo 1 o ninguno del mismo color que el centro, ya que entonces se podría unir los vértices del otro color de la misma forma que hicimos cuando había tres de un color y 3 de otro alternativo.
El caso más complejo es aquel en el que hay 2 vértices del mismo color que el centro, y 4 del color opuesto. Evidentemente, los del mismo color no pueden ser consecutivos, con lo que puede haber sólo dos situaciones diferentes: en la primera, si entre ambos hay un único vértice de color distinto, se puede unir de la misma forma que en el caso 3 y 3, y en la segunda hay dos vértices entre ambos del mismo color que el centro, de forma simétrica. Trataremos este caso de una forma más detallada, porque es el más complejo y el único que queda.
En ese caso especial el hexágono central de la estrella aparecen dos vértices opuestos del mismo color que el centro y los otros cuatro de color contrario. Es evidente que entre los puntos citados hasta ahora no hay un triángulo equilátero con los vértices del mismo color. Consideremos una de las puntas de la estrella, una de las dos que esté unida a los vértices de color contrario al centro. No puede ser del mismo color que ellos (distinto del centro), ya que formaría un triángulo equilátero con ellos, pero tampoco del color del centro, ya que formaría un triángulo equilátero con los dos vértices del hexágono que son del mismo color (el centro pertenecería a uno de los lados del triángulo).
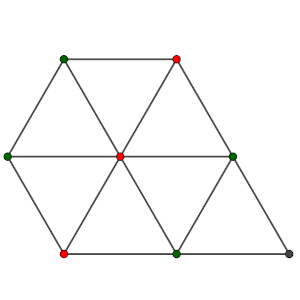
Por lo tanto, en cualquier coloreado existe al menos un triángulo equilátero. De hecho, en realidad podríamos hacer la misma demostración con 3 puntos menos, eligiendo cuidadosamente los puntos a eliminar (hay dos formas diferentes, una de ellas triangular).
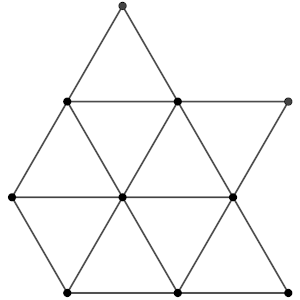
Holi