Invirtiendo las reglas
Problema 10 del concurso Marató de problemes 2022 Se dirige a una edad de: 14-15 años
Aplicamos una de las siguientes reglas a un número positivo n:
Si n es impar, lo incrementamos 5 unidades, pasamos a n + 5.
Si n es par, lo dividimos por 2, y por tanto pasamos a n/2.
Aplicamos esta regla a un número entero k y obtenemos r.
Después aplicamos la regla a r y obtenemos s.
Finalmente aplicamos la regla a s y obtenemos t.
Si resulta que t es 2022, ¿cuál es el valor más pequeño que puede tener el número inicial k?

Solución: Aquí.
Solución a ecuación diofántica
Problema 9 del concurso Marató de problemes 2022 Se dirige a una edad de: 14-15 años
¿Cuántas soluciones diferentes tiene la ecuación 9x + 2y + 3z = 59, en la que x, y, z son números enteros positivos?
¿Cuál es el mayor valor que toma x + y + z para alguna de estas soluciones?
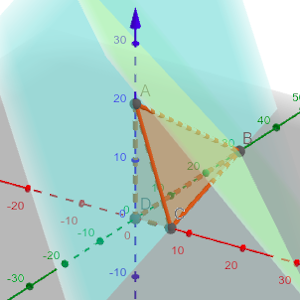
Solución:
(more…)
Ecuación diofántica
Problema 9 del concurso Marató de problemes 2022 Se dirige a una edad de: 14-15 años
¿Cuántas soluciones diferentes tiene la ecuación 9x + 2y + 3z = 59, en la que x, y, z son números enteros positivos?
¿Cuál es el mayor valor que toma x + y + z para alguna de estas soluciones?

Solución: Aquí.
Solución a dígitos en espiral
Problema 8 del concurso Marató de problemes 2022 Se dirige a una edad de: 14-15 años
Los dígitos de la secuencia 123451234512345… (sucesivas copias de los cinco dígitos 12345) se sitúan en las celdas de una cuadrícula formando una cadencia en espiral que comienza en la celda marcada en gris, tal y como mostramos en la siguiente imagen.
a) Explica en qué casilla estará situado el 5 que ocupa el lugar 80 de la secuencia.
b) Expón un algoritmo adecuado para situar en la cuadrícula la cifra que ocupa el lugar n de la secuencia.
c) Razona qué dígito estará colocado exactamente 15 celdas por encima de la celda marcada en gris.
d) Expón un algoritmo adecuado para decidir qué cifra ocupa la casilla que está “en vertical” exactamente c celdas por encima de la casilla gris.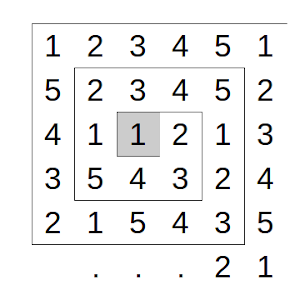
Solución:
(more…)
Dígitos en espiral
Problema 8 del concurso Marató de problemes 2022 Se dirige a una edad de: 14-15 años
Los dígitos de la secuencia 123451234512345… (sucesivas copias de los cinco dígitos 12345) se sitúan en las celdas de una cuadrícula formando una cadencia en espiral que comienza en la celda marcada en gris, tal y como mostramos en la siguiente imagen.
a) Explica en qué casilla estará situado el 5 que ocupa el lugar 80 de la secuencia.
b) Expón un algoritmo adecuado para situar en la cuadrícula la cifra que ocupa el lugar n de la secuencia.
c) Razona qué dígito estará colocado exactamente 15 celdas por encima de la celda marcada en gris.
d) Expón un algoritmo adecuado para decidir qué cifra ocupa la casilla que está “en vertical” exactamente c celdas por encima de la casilla gris.
Solución: Aquí.
Solución a la base de la pirámide
Problema 7 del concurso Marató de problemes 2022 Se dirige a una edad de: 14-15 años
Una pirámide recta de h centímetros de altura tiene como base una de las caras de un cubo.
La suma de las longitudes de las aristas de la pirámide es igual a la suma de las longitudes de todas las aristas del cubo.
¿Cuál es el área de la base de la pirámide? (Se debe dar en función de h)
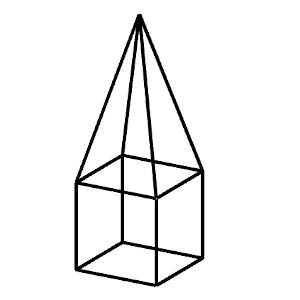
Solución:
(more…)
La base de la pirámide
Problema 7 del concurso Marató de problemes 2022 Se dirige a una edad de: 14-15 años
Una pirámide recta de h centímetros de altura tiene como base una de las caras de un cubo.
La suma de las longitudes de las aristas de la pirámide es igual a la suma de las longitudes de todas las aristas del cubo.
¿Cuál es el área de la base de la pirámide? (Se debe dar en función de h)

Solución: Aquí.
Solución a 16 baldosas
Problema 6 del concurso Marató de problemes 2022 Se dirige a una edad de: 14-15 años
Disponemos de dieciséis baldosas cuadradas en las que aparecen dos cuartos de circunferencia centradas en esquinas opuestas cuyo radio es la mitad del lado de la baldosa.
Con ellas formamos un cuadrado, como en la imagen del ejemplo.
Veréis que en esta imagen hay una línea curva que conecta 12 de los arcos que hay, otra conecta 6 y otra conecta 5.
¿Cuál es el número máximo de arcos que podemos conectar en una curva cuando creamos el cuadrado de 16 baldosas?
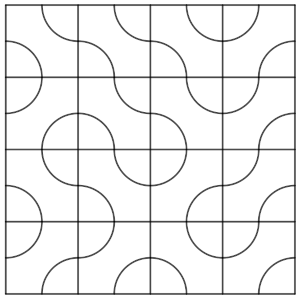
Solución:
(more…)