Problema 8 del concurso Marató de problemes 2022 Se dirige a una edad de: 14-15 años
Los dígitos de la secuencia 123451234512345… (sucesivas copias de los cinco dígitos 12345) se sitúan en las celdas de una cuadrícula formando una cadencia en espiral que comienza en la celda marcada en gris, tal y como mostramos en la siguiente imagen.
a) Explica en qué casilla estará situado el 5 que ocupa el lugar 80 de la secuencia.
b) Expón un algoritmo adecuado para situar en la cuadrícula la cifra que ocupa el lugar n de la secuencia.
c) Razona qué dígito estará colocado exactamente 15 celdas por encima de la celda marcada en gris.
d) Expón un algoritmo adecuado para decidir qué cifra ocupa la casilla que está “en vertical” exactamente c celdas por encima de la casilla gris.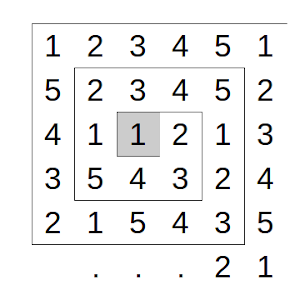
Solución:
Evidentemente, los dígitos situados en posición 5, 10, 15, y cualquier múltiplo de 5, serán iguales a 5.
Ahora, vamos a calcular las coordenadas en las que está situado el dígito número 80.
Como se puede ver en la imagen, la forma en la que vamos situando los dígitos es formando cuadrados cada vez mayores, es decir, que los 4 primeros dígitos formarán un cuadrado de lado 2, los 9 primeros dígitos formarán un cuadrado de lado 3, y así sucesivamente.
Si no nos hemos dado cuenta de ese detalle, conviene idear una espiral similar poniendo la posición correspondiente, y atender a las formas cuadradas, es decir, “completas”.
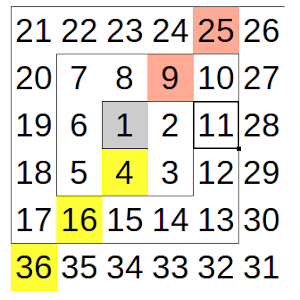
Como resulta que 80 es un número que está delante de un cuadrado, el 81, es mejor situar el número 81 primero, y calcular dónde va el anterior.
Si nos fijamos en el dibujo anterior, los cuadrados impares están situados siguiendo una diagonal desde la casilla marcada en gris, hacia arriba y hacia la derecha, mientras que los cuadrados pares se sitúan siguiendo una diagonal hacia abajo y hacia la izquierda con respecto a la casilla que ocupa el primer 4, inmediatamente debajo de la casilla gris.
Puesto que 81 es el cuadrado de 9, que es el quinto impar, estará situado 4 casillas por encima de la casilla gris, y 4 casillas hacia la derecha. Por eso, el 5 que ocupa el lugar 80 de la secuencia, estará en la casilla situada 4 por encima y 3 hacia la derecha de la casilla gris.
El algoritmo que creo que es más asequible es tomar la parte entera de la raíz del lugar que queramos calcular, a la que podemos llamar q, y la diferencia desde q² hasta el lugar n, que podemos llamar p.
Si q es par, en el caso en el que p sea 0, estaríamos en la posición q/2 por debajo de la casilla gris, y q/2 – 1 a la izquierda. Ahora, todo depende de si p es mayor que n, o no.
Si p es mayor que 0, y menor o igual que q, la posición correcta será q/2 + 1 – p por debajo de la casilla gris (en caso de que p sea mayor que q/2, será p – q/2 – 1 por arriba), y exactamente q/2 a la izquierda. Le llamo caso 1.
Si p es mayor que q, está limitado por 2q, ya que q² + 2q + 1 es el cuadrado de q + 1, por lo que q debería ser mayor. En ese caso, su posición será q/2 por encima de la casilla gris, y q/2 + q + 1 – p a la izquierda de la casilla gris, salvo que p sea mayor que q + q/2, en cuyo caso será p – q – q/2 – 1 a la derecha de la casilla gris. Le llamo caso 2.
Si q es impar, el cálculo es muy diferente. En el caso en que p sea 0, tendríamos la posición (q – 1)/2 por arriba de la casilla gris, y (q – 1)/2 a la derecha de la casilla gris.
Si p es mayor que 0, y menor o igual que q, la posición correcta sería (q – 1)/2 + 1 – p por encima de la casilla gris, aunque si p es mayor que (q – 1)/2, estaría p – (q – 1)/2 – 1 por debajo de la casilla gris, y en cualquier caso, (q – 1)/2 + 1 a la derecha de la casilla gris. Le llamo caso 3.
Si p es mayor que q, está limitado a 2q (de nuevo, por ser q² + 2q + 1 un cuadrado perfecto), y la posición vertical sería (q – 1)/2 + 1 por debajo de la casilla gris, y (q – 1)/2 + 2 + q – p a la derecha de la casilla gris (salvo que p sea mayor que (q – 1)/2 + 2 + q, porque en ese caso sería p – (q – 1)/2 – 2 – q a la derecha de la casilla gris. Le llamo caso 4.
Vamos a comprobar algunas casillas con el ejemplo que tenemos en el dibujo, porque así es como he perfilado un poco las fórmulas correspondientes a los cuatro lados. Se podría haber perfilado un poco las opciones, haciendo la raíz de uno menos del lugar en lugar de la raíz del lugar, para evitar tener que ocuparse de la posición 0, pero creo que queda más claro así.
Por ejemplo, el elemento 15 está dos casillas por debajo y 0 a la izquierda o a la derecha de la casilla gris. En este caso, q es la parte entera de la raíz cuadrada, que sería 3, que es impar, y p vale 6, es decir, es mayor que q. Así que estaríamos en el cuarto caso, q es impar, y p es mayor que q. Su posición vertical sería (3 – 1)/2 + 1 = 2 por debajo de la casilla gris, y (3 – 1)/2 + 2 + 3 – p = 0 a la derecha, en efecto.
Otro ejemplo, el 29, que está 3 a la derecha y 1 por debajo de la casilla gris. La parte entera de la raíz es 5, y p en este caso vale 4, que es menor que q. Estaríamos en el caso 3. Según el algoritmo, puesto que p es mayor que (q – 1)/2 = 2, estaría p – (q – 1)/2 – 1 = 1 por debajo de la casilla gris y (q – 1)/2 + 1 = 3 a la derecha, efectivamente.
Un tercer ejemplo sería el 18, dos casillas a la izquierda y una por debajo. La parte entera de la raíz cuadrada, q, valdría 4, que es par, y p sería 2, menor que q. El caso sería el 1. Su posición sería q/2 + 1 – p = 1 por debajo de la casilla gris, y exactamente q/2 = 2 a la izquierda.
Y el cuarto ejemplo de referencia sería el 24 (dos arriba y una a la derecha), en el que q = 4 y p = 8, mayor que q, es decir, el caso 2, su posición será q/2 = 2 por encima de la casilla gris y, como p es mayor que q + q/2 + 1 = 6, en cuyo caso será p – q – q/2 – 1 = 1 a la derecha de la casilla gris.
Veamos ahora el apartado c. Se trata de encontrar el número que hay en la casilla 15 por encima de la gris. Es relativamente fácil encontrar el número que va en esa posición, de nuevo fijándonos en la diagonal de los cuadrados. El cuadrado que corresponde a 15 la derecha y 15 por arriba de la gris, sería el 31² = 961, ya que 31 es el impar número 16. Puesto que queremos el que hay en la posición 0 a la derecha, en lugar de 15 a la derecha, se tratará del número 961 – 15 = 946 el que ocupa esa posición, así que se tratará del dígito 1, por ser 945 divisible por 5.
Encontrar un algoritmo que describa el número que aparece en la casilla c celdas por encima de la casilla gris, a partir de lo que hemos visto en el apartado anterior, es relativamente sencillo. El cuadrado que corresponde a c por arriba y c a la derecha es (2c + 1)², y como la posición que buscamos está desplazada c a la derecha, el dígito que deberemos situar es el que corresponde a la posición (2c + 1)² – c = 4c² + 3c + 1.
Y este dígito debemos leerlo en módulo 5, es decir, según su resto al dividirlo por 5. Cada 5 unidades volverá a ser el mismo, ya que c², módulo 5, sigue un ritmo determinado (1, 4, 4, 1, 0, 1, 4, 4, 1, …), 4c² seguirá también un ritmo (4, 1, 1, 4, 0, 4, 1, 1, 4, 0, …). Por otra parte, 3c sigue el patrón (3, 1, 4, 2, 0, 3, 1, 4, 2, 0, …), y al sumarle a estos ritmos 1 obtendremos (3, 3, 1, 2, 1, 3, 3, 1, 2, 1, …) (no lo hay, pero si hubiese algún caso en el que el que módulo 5 sea 0, quiere decir que esa celda la ocupa en realidad un 5).
Por tanto, el algoritmo más eficaz para decidir cuál es el número que ocupa la posición c por encima de la casilla gris, sería el siguiente: Determinar el resto al dividir c entre 5, y en cada una de las posibilidades, obtendremos lo siguiente:
Si el resto es 1, el dígito será un 3.
Si el resto es 2, el dígito será un 3.
Si el resto es 3, el dígito será un 1.
Si el resto es 4, el dígito será un 2.
Si el resto es 0, el dígito será un 1.
Esto encaja con los números que hemos obtenido en el ejemplo inicial, y también en el ejemplo estudiado en el apartado anterior. De hecho, compararlo con los ejemplos me ha servido para corregir algunos errores de cálculo.