Un juego justo
Problema 1 del reto de selección para el MathCamp de Estados Unidos y Canadá (2018) Se dirige a una edad de: 14-17 años
João y Kinga juegan a un juego con un dado justo de n caras, que están numeradas del 1 al n. En este juego, a João se le asigna un valor j y a Kinga un valor k, ambos en rango del 1 al n. João y Kinga se turnan lanzando el dado, empezando a lanzarlo João.
Si João obtiene un número menor o igual que j, el juego acaba y él gana. Si Kinga obtiene un número menor o igual que k, entonces gana Kinga y el juego acaba. El juego continúa hasta que uno de los dos jugadores gana.
Demuestra que si j = k, entonces João siempre tiene ventaja.
Si n = 6, encuentra todos los posibles valores de j y k que hacen el juego justo (es decir, que hacen que tanto João como Kinga tengan una probabilidad de un 50% de ganar).
Si n = 101, demuestra que ningún valor de j y k hacen el juego justo.
Solución: Aquí.
Solución a números que contienen una suma
Problema 2 del segundo nivel de la Olimpiada de Mayo (2017) Se dirige a una edad de: 14 años
Varios números reales diferentes están escritos en la pizarra.
Si a, b y c son tres de estos números, al menos una de las siguientes sumas: a + b, a + c, b + c, también es uno de los números escritos en la pizarra.
¿Cuál es la mayor cantidad posible de números escritos en la pizarra?
Solución:
(more…)
Números que contienen una suma
Problema 2 del segundo nivel de la Olimpiada de Mayo (2017) Se dirige a una edad de: 14 años
Varios números reales diferentes están escritos en la pizarra.
Si a, b y c son tres de estos números, al menos una de las siguientes sumas: a + b, a + c, b + c, también es uno de los números escritos en la pizarra.
¿Cuál es la mayor cantidad posible de números escritos en la pizarra?
Solución: Aquí.
Solución a juego con dos colores
Problema 4 del primer nivel de la Olimpiada de Mayo (2017) Se dirige a una edad de: 12 años
Sea n un entero par mayor que 2.
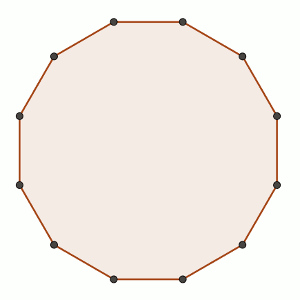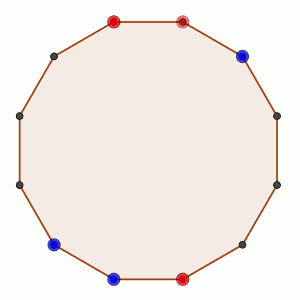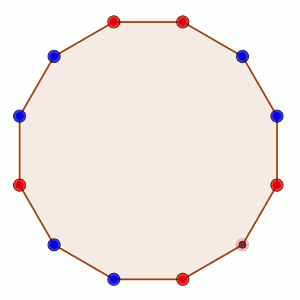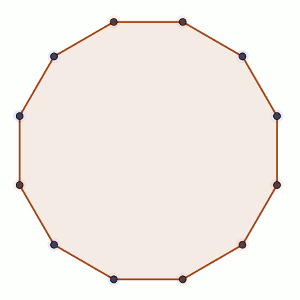
Sobre los vértices de un polígono regular de n lados se pueden colocar fichas rojas o azules.
Dos jugadores, A y B juegan alternándose turnos del siguiente modo: cada jugador, en su turno, elige dos vértices que no tengan fichas y coloca en uno de ellos una ficha roja y en el otro una azul.
El objetivo de A es conseguir que haya tres vértices consecutivos con fichas del mismo color, mientras que el objetivo de B es impedir que esto suceda.
Al comienzo del juego no hay fichas en ninguno de los vértices.
Demostrar que, independientemente de quién empiece a jugar, el jugador B siempre podrá conseguir su objetivo.
Solución:
(more…)
Juego con dos colores
Problema 4 del primer nivel de la Olimpiada de Mayo (2017) Se dirige a una edad de: 12 años
Sea n un entero par mayor que 2.
Sobre los vértices de un polígono regular de n lados se pueden colocar fichas rojas o azules.
Dos jugadores, A y B juegan alternándose turnos del siguiente modo: cada jugador, en su turno, elige dos vértices que no tengan fichas y coloca en uno de ellos una ficha roja y en el otro una azul.
El objetivo de A es conseguir que haya tres vértices consecutivos con fichas del mismo color, mientras que el objetivo de B es impedir que esto suceda.
Al comienzo del juego no hay fichas en ninguno de los vértices.
Demostrar que, independientemente de quién empiece a jugar, el jugador B siempre podrá conseguir su objetivo.

Solución: Aquí.
Solución a las reglas de ababa
Problema 5 del segundo nivel de la Olimpiada de Mayo (2017) Se dirige a una edad de: 14 años
Ababa juega con una palabra formada con las letras de su nombre, y se ha puesto ciertas reglas:
Si encuentra una A seguida inmediatamente por una B, las puede sustituir por BAA.
Si encuentra dos B consecutivas, las puede borrar.
Si encuentra tres A consecutivas, las puede borrar.
Ababa empieza con la palabra ABABABAABAAB.
Con las reglas anteriores ¿Cuántas letras tiene la palabra más corta a la que puede llegar?
¿Por qué no puede llegar a una palabra más corta?

Solución:
(more…)
Los resultados de la Olimpiada Internacional de Matemáticas 2018
Se trata de la principal competición internacional para aficionados a la resolución de problemas matemáticos de todo el mundo. En esta ocasión, celebra su edición número 59.
Los participantes se enfrentan a 6 complicados problemas durante 7 horas, en dos bloques de tres problemas (tres horas y media), dos días consecutivos. Cada problema resuelto, entre los que abundan los problemas en los que hay que demostrar un enunciado, debe estar correctamente razonado, y se puntúa entre 0 y 7 puntos. Por tanto, la puntuación perfecta es de 42 puntos.
La corrección es un proceso cuidadosamente orquestado. Cada hoja que escribe cada participante es copiada, la original queda en manos de los coordinadores, y la copia en manos del jefe de delegación. Hay una reunión posterior, llamada coordinación, en la que ambos (jefe de delegación de cada país y los coordinadores especialistas en cada uno de los seis problemas) acuerdan la cantidad de puntos concedidos en cada problema a cada participante.
A título individual, destacaremos que dos participantes han logrado la puntuación perfecta, 42 puntos, quedando clasificados como los ganadores, un estadounidense, James Lin, y un participante del Reino Unido, Agnijo Banerjee. Se da la circunstancia de que James ha sido seleccionado por segunda vez, cosa que indica la extraordinaria preparación del candidato, que el año pasado obtuvo un meritorio sexto puesto.
En tercer lugar encontramos otro estadounidense, Mihir Anand Singhal, que sólo perdió 2 puntos en el problema 3, uno de los dos más complicados en teoría de la prueba.
Empatados a 39 puntos, en cuarto y quinto lugar, encontramos a Marat Abdrakhmanov, de la Federación Rusa y a Shih-Yu Wang, de Taiwan. Los problemas en los que perdieron los 3 puntos fueron, de nuevo, el tercero y el sexto, los teóricamente más duros. El participante de Taiwan acude a la prueba por tercera vez, habiendo obtenido ya dos medallas de plata, además del oro de este año.
En sexto lugar (empatado con séptimo, y octavo) encontramos a Jonas Walter, de Alemania. En su segunda participación (en la anterior obtuvo bronce) sólo perdió 4 puntos en el problema 3, también encontramos a Naoki Kuroda, de Japón, de nuevo segunda participación, pero segundo oro, y Jung-Tao Cheng, también de Taiwan, que, curiosamente, perdió puntos en el quinto en lugar de en los dos más difíciles a priori.
Algo más abajo, en la posición 12-18, encontramos a Pedro Lucas Lanaro Sponchiado, primer clasificado iberoamericano, de Brasil. Obtuvo 35 puntos, perdiendo seis puntos en el problema tres y un punto en el supuestamente más sencillo problema uno.
Si bajamos hasta la posición 19-23, aunque todavía considerado oro, encontramos la primera mujer, una tailandesa llamada Yolrada Yongpisanpob, que en su única participación sólo ha perdido cuatro puntos en cada uno de los dos problemas más difíciles. Todavía es baja la participación femenina en la prueba internacional (60 concursantes de un total de 594, un 10% aproximadamente), así que es muy meritorio lograr estas posiciones. A propósito de esto, un par de curiosidades, entre los 60 participantes de los 10 países que quedan en las 10 primeras posiciones sólo encontramos 4 participantes femeninas, y entre los 107 países sólo 4 participan con 3 hombres y 3 mujeres (Lituania, la Ex República Yugoslava de Macedonia, Botswana y Camboya) y en ninguna delegación hay más mujeres que hombres.
Mucho mérito tiene también Mohammad Sharifi Kiasari, de la República Islámica de Irán, que, pese a proceder de un país en guerra, ha obtenido una posición de medalla de oro (27-33), con 32 puntos, cuatro problemas perfectos y cuatro puntos obtenidos en los dos más difíciles.
En las últimas medallas de oro, las posiciones 34-48, con 31 puntos, encontramos al primer francés, Paul Cahen, y a la segunda mujer, Dain Kim, de la República de Corea.
Entre los ganadores de la medalla de plata hay varios hablantes de nuestra lengua, el primer argentino, Julián Masliah. Víctor Antonio Domínguez Silva, de México, Diego Lázaro Cusihuaman y Joseph Daniel Altamirano Pacheco, de Perú.
Los españoles han logrado un buen resultado para los precedentes que había, dos medallas de bronce (Santiago Vázquez Sáez, 17 puntos y Alejandro Epelde Blanco, 16 puntos) y cuatro menciones honoríficas, lo que significa que han quedado por debajo de las posiciones de medalla (en este caso 16 puntos, algo más de dos problemas perfectos), pero han conseguido resolver al menos uno de los problemas.
Aunque de forma extraoficial, hay una clasificación por equipos, que en esta ocasión la encabeza Estados Unidos de América (5 oros y una plata), la Federación Rusa (5 oros y una plata) y la República Popular China (4 oros y 2 platas).
El primer país europeo es Polonia, en novena posición con un oro y 5 platas, aunque el Reino Unido no queda muy atrás, décimo segundo con un oro, cuatro platas y una mención honorífica.
Brasil es el primer país iberoamericano (puesto 28-30, empatado con India y Mongolia), con una plata, cuatro bronces y una mención, justo delante de Alemania. Perú, en la posición 35, con dos platas, tres bronces y una mención, y México, en la posición 36-37 (empatado con Países Bajos), con una plata, cuatro bronces y una mención, la siguen. Algo por debajo está Argentina (posición 39-40, empatada con la República Checa), con una plata y cuatro bronces.
España queda en posición 55-56, empatada con Grecia y un puesto por debajo de Portugal.
Finlandia, tan popularmente citada en el campo de la educación, queda en la posición 59. Contrasta con otro país muy citado en este tema, Singapur, que, también con una cantidad de población (unos cinco millones de personas) muy inferior a la española, obtiene un envidiable octavo puesto (dos oros, tres platas y un bronce).
Las reglas de ababa
Problema 5 del segundo nivel de la Olimpiada de Mayo (2017) Se dirige a una edad de: 14 años
Ababa juega con una palabra formada con las letras de su nombre, y se ha puesto ciertas reglas:
Si encuentra una A seguida inmediatamente por una B, las puede sustituir por BAA.
Si encuentra dos B consecutivas, las puede borrar.
Si encuentra tres A consecutivas, las puede borrar.
Ababa empieza con la palabra ABABABAABAAB.
Con las reglas anteriores ¿Cuántas letras tiene la palabra más corta a la que puede llegar?
¿Por qué no puede llegar a una palabra más corta?

Solución: Aquí.
Solución a ascendente múltiplo de 56
Problema 1 del segundo nivel de la Olimpiada de Mayo (2017) Se dirige a una edad de: 14 años
Decimos que un número entero positivo es ascendente si sus cifras, leídas de izquierda a derecha, están en orden estrictamente creciente. Por ejemplo, 458 es ascendente, mientras que 2339 no lo es.
Hallar el mayor número ascendente que es múltiplo de 56.
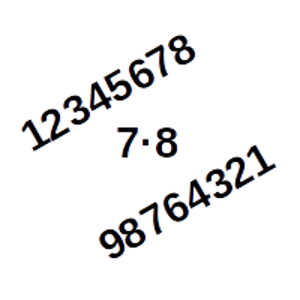
Solución:
(more…)
Ascendente múltiplo de 56
Problema 1 del segundo nivel de la Olimpiada de Mayo (2017) Se dirige a una edad de: 14 años
Decimos que un número entero positivo es ascendente si sus cifras, leídas de izquierda a derecha, están en orden estrictamente creciente. Por ejemplo, 458 es ascendente, mientras que 2339 no lo es.
Hallar el mayor número ascendente que es múltiplo de 56.
Solución: Aquí.