Problema 4 del primer nivel de la Olimpiada de Mayo (2017)
Se dirige a una edad de: 12 años

Sea n un entero par mayor que 2.

Sobre los vértices de un polígono regular de n lados se pueden colocar fichas rojas o azules.

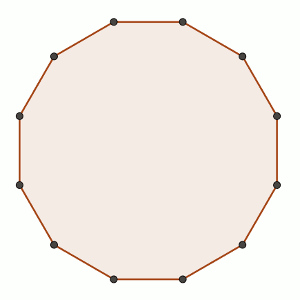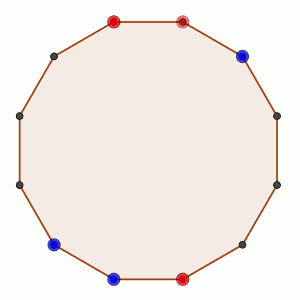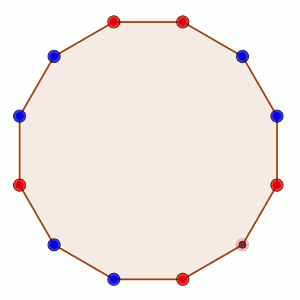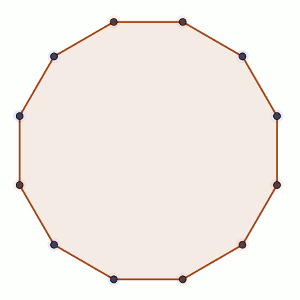
Dos jugadores, A y B juegan alternándose turnos del siguiente modo: cada jugador, en su turno, elige dos vértices que no tengan fichas y coloca en uno de ellos una ficha roja y en el otro una azul.

El objetivo de A es conseguir que haya tres vértices consecutivos con fichas del mismo color, mientras que el objetivo de B es impedir que esto suceda.

Al comienzo del juego no hay fichas en ninguno de los vértices.

Demostrar que, independientemente de quién empiece a jugar, el jugador B siempre podrá conseguir su objetivo.

Solución:

Se trata de crear una estrategia sencilla. Realmente, de crear una estrategia para impedir que otro pueda llevar a cabo la suya.

Al tratarse de una cantidad par, y buscar impedir colores consecutivos, una idea rápida es tratar siempre con pares de casillas.

El jugador B puede tratar, durante todas sus jugadas de que cualquier par de casillas consecutivas (impar-par) tengan una ficha de cada color. De esta forma, a lo sumo hay dos casillas ocupadas por fichas del mismo color.

Esto es fácil de conseguir. Si antes de jugar B todas las casillas impar-par están ocupadas por una ficha de diferente color, o vacías, entonces elige una pareja de casillas contiguas impar-par vacías y pone una ficha de cada color. Y si esto no es así, es porque en la jugada anterior, el A ha cambiado una situación de equilibrio, poniendo dos fichas de diferente color en dos parejas de tipo impar-par diferentes. El jugador B, en ese caso, elegirá las parejas correspondientes a la jugada de A y las anulará poniendo los colores contrarios, de forma que ambas parejas impar-par tendrán una ficha de cada color.

En este tipo de estrategias, lo importante es mantener la simetría, es decir, no dejar nunca que el rival cree una situación en la que pueda tender una trampa.

No he podido analizar si para un número de casilla impar, cambiando ligeramente el juego, existe una estrategia. Me gustaría ver uno de esos programas de inteligencia artificial (o de aprendizaje artificial) descubrir una estrategia ganadora para un juego sencillo como éste. No dudo que podría hacerse sin dificultad, ya que Alfago Zero ha conseguido aprender a jugar al Go, que es muchísimo más complicado, pero me gustaría ver si aplican una estrategia sencilla u optan por una mucho más compleja e imprevisible.