Arrinconadas
Problema 5 de la fase catalana de la 57 Olimpiada Matemática Española (2020/21) Se dirige a una edad de: 16-17 años
Ana y Bernat juegan un juego sobre un tablero ajedrezado de dimensiones 2020×2020.
Decimos que una colección de piezas puestas en ese tablero está arrinconada (en la esquina inferior izquierda) si no hay ninguna casilla vacía de forma que la casilla inmediatamente superior o inmediatamente a la derecha de ella contenga una pieza, como se muestra en la figura.
Inicialmente, hay 2020 piezas colocadas en una posición arrinconada.
En turnos alternos, comenzando por Ana, cada jugador retira dos piezas de casillas adyacentes (con un lado en común), con la condición de que la configuración restante siga siendo arrinconada.
Pierde el jugador que no puede hacer un movimiento.
Determina cuál de los dos jugadores ganará en función de la posición inicial de las 2020 piezas, suponiendo que ambos jueguen de forma óptima.

Solución: Aquí.
Solución a un tablero cuadrado
Problema 2 de la fase catalana de la 57 Olimpiada Matemática Española (2020/21) Se dirige a una edad de: 16-17 años
Tenemos un tablero nxn, con n > 2.
Escribimos en cada casilla un número natural entre el 1 y el n² diferente, en cualquier orden.
Demuestra que siempre existen dos casillas adyacentes tales que los números que x, y que contienen satisfacen la siguiente desigualdad: |x – y| ≥ n/2 + 1.
Entendemos que son casillas adyacentes aquellas que comparten un lado.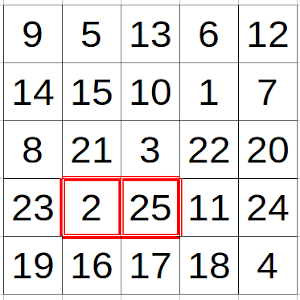
Solución:
(more…)
Un tablero cuadrado
Problema 2 de la fase catalana de la 57 Olimpiada Matemática Española (2020/21) Se dirige a una edad de: 16-17 años
Tenemos un tablero nxn, con n > 2.
Escribimos en cada casilla un número natural entre el 1 y el n² diferente, en cualquier orden.
Demuestra que siempre existen dos casillas adyacentes tales que los números que x, y que contienen satisfacen la siguiente desigualdad: |x – y| ≥ n/2 + 1.
Entendemos que son casillas adyacentes aquellas que comparten un lado.
Solución: Aquí.
Solución a fracciones irreducibles
Problema 4 de la fase catalana de la 57 Olimpiada Matemática Española (2020/21) Se dirige a una edad de: 16-17 años
Determina todos los valores enteros de n tales que la fracción (8n – 3)/(17n – 9) es irreducible.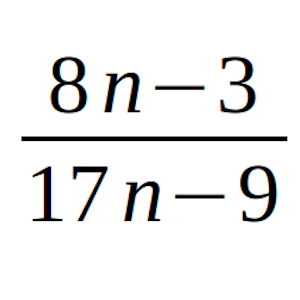
Solución:
(more…)
Fracciones irreducibles
Problema 4 de la fase catalana de la 57 Olimpiada Matemática Española (2020/21) Se dirige a una edad de: 16-17 años
Determina todos los valores enteros de n tales que la fracción (8n – 3)/(17n – 9) es irreducible.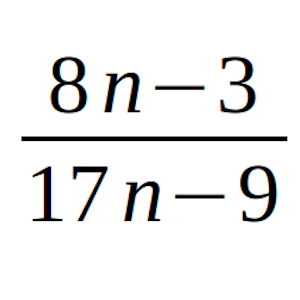
Solución: Aquí.
Solución a entre 1010 y 2020
Problema 1 de la fase catalana de la 57 Olimpiada Matemática Española (2020/21) Se dirige a una edad de: 16-17 años
Sean a y b dos números reales tales que 1010 ≤ a, b ≤ 2020.
Demuestra que (a + b)(1/a + 1/b) ≤ 9/2.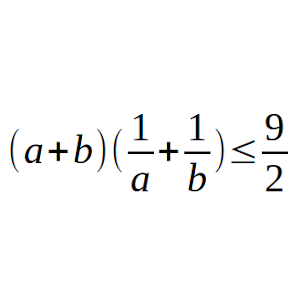
Solución:
(more…)
Entre 1010 y 2020
Problema 1 de la fase catalana de la 57 Olimpiada Matemática Española (2020/21) Se dirige a una edad de: 16-17 años
Sean a y b dos números reales tales que 1010 ≤ a, b ≤ 2020.
Demuestra que (a + b)(1/a + 1/b) ≤ 9/2.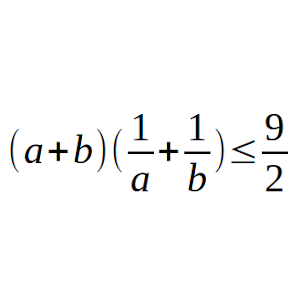
Solución: Aquí.
Solución a malas fichas
Problema 3 de la fase nacional de la 57 Olimpiada Matemática Española (2021) Se dirige a una edad de: 16-17 años
Tenemos 2021 colores y 2021 fichas de cada color.
Colocamos las 2021² fichas en fila.
Se dice que una ficha F es “mala” si a cada lado queda un número impar de las 2020·2021 fichas que no comparten color con F.
(a) Determina cuál es el mínimo número posible de fichas malas.
(b) Si se impone la condición de que cada ficha ha de compartir color con al menos una ficha adyacente. ¿Cuál es el mínimo número posible de fichas malas?
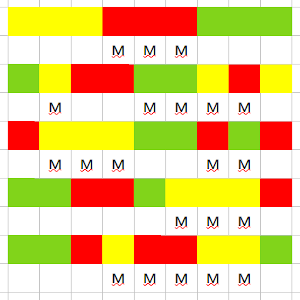
Solución:
(more…)
Malas fichas
Problema 3 de la fase nacional de la 57 Olimpiada Matemática Española (2021) Se dirige a una edad de: 16-17 años
Tenemos 2021 colores y 2021 fichas de cada color.
Colocamos las 2021² fichas en fila.
Se dice que una ficha F es “mala” si a cada lado queda un número impar de las 2020·2021 fichas que no comparten color con F.
(a) Determina cuál es el mínimo número posible de fichas malas.
(b) Si se impone la condición de que cada ficha ha de compartir color con al menos una ficha adyacente. ¿Cuál es el mínimo número posible de fichas malas?

Solución: Aquí.