Problema 2 de la fase catalana de la 57 Olimpiada Matemática Española (2020/21) Se dirige a una edad de: 16-17 años
Tenemos un tablero nxn, con n > 2.
Escribimos en cada casilla un número natural entre el 1 y el n² diferente, en cualquier orden.
Demuestra que siempre existen dos casillas adyacentes tales que los números que x, y que contienen satisfacen la siguiente desigualdad: |x – y| ≥ n/2 + 1.
Entendemos que son casillas adyacentes aquellas que comparten un lado.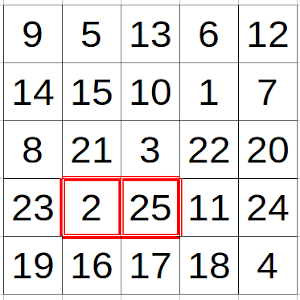
Solución:
La cuestión es que resulta fácil comprobarlo en los tableros pequeños. Si tratamos de poner los números del 1 al 9 en un tablero 3×3, pronto comprobamos que es imposible ponerlos sin que superen la distancia 2,5 (es decir, alcancen el 3) en algún momento.
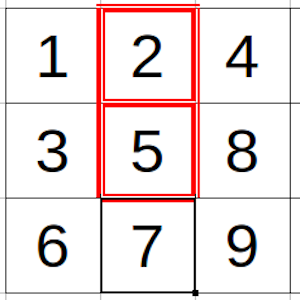
La jugada clave si intentamos situar los números con la menor diferencia posible es tratar de que lo números que están en posiciones contiguas sean lo más parecidos entre sí, pero para lograr esto los números más extremos (en nuestro ejemplo, el 1 y el 9) deben estar en posiciones lo más lejanas posibles, e ir creciendo poco a poco de uno a otro.
De ahí, podemos establecer un camino de celdas contiguas que una los extremos, entre 1 y n².
Este camino de celdas contiguas debe tener como mucho 2n – 1 casillas, ya que el peor caso es que estén en posiciones que ocupan las esquinas del tablero (como en el ejemplo) y que los caminos deban recorrer todas las casillas horizontalmente y verticalmente. Eso significa que debe tener n casillas horizontalmente y n – 1 para “conectar” una a otra.
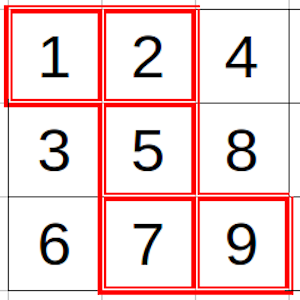
Razonando entonces por reducción al absurdo, si suponemos que todas las casillas cumplen la condición contraria, es decir, |x – y| es menor que n/2 + 1, seguro que las casillas que ocupan las celdas que forman ese camino mínimo son todas menores que una progresión aritmética que comienza por 1, de 2n – 1 términos que estuvieran a menos de esa distancia de n/2 + 1, es decir que la última casilla, ocupada por n² sería menor que 1 + d(2n – 2).
Si estamos hablando de un número n par, d puede ser a lo sumo n/2, por lo que n² ≤ 1 + (2n – 2)n/2 = 1 + n² – n, claramente imposible, puesto que n es mayor que 2.
Si estamos hablando de un número impar, d puede ser a lo sumo (n + 1)/2, luego n² ≤ 1 + (2n – 2)(n + 1)/2 = 1 + (2n² – 4)/2 = n². Esta circunstancia sí sería posible, pero obligaría a que toda la secuencia estaría formada por los términos de esa progresión aritmética. Es decir, el primer término sería 1, el segundo, 1 + (n + 1)/2, y así sucesivamente (de hecho, en nuestro ejemplo se puede escoger un camino como ese), pero en ese caso, puesto que 1 y n² estarían en esquinas contrarias del tablero, podríamos tomar otro camino diferente, por ejemplo, tomando una casilla a la derecha en lugar de hacia abajo al salir del 1, o viceversa, y los números deberían entonces ser diferentes y el destino debería ser al menos una unidad mayor, cosa que es imposible.
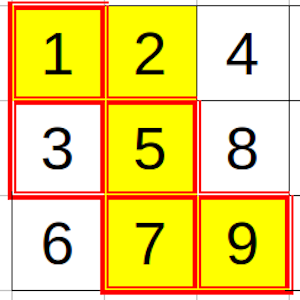
Por lo tanto, por reducción al absurdo, existen esos dos números contiguos con una diferencia de al menos n/2 + 1.