Problema 3 de la fase nacional de la 57 Olimpiada Matemática Española (2021) Se dirige a una edad de: 16-17 años
Tenemos 2021 colores y 2021 fichas de cada color.
Colocamos las 2021² fichas en fila.
Se dice que una ficha F es “mala” si a cada lado queda un número impar de las 2020·2021 fichas que no comparten color con F.
(a) Determina cuál es el mínimo número posible de fichas malas.
(b) Si se impone la condición de que cada ficha ha de compartir color con al menos una ficha adyacente. ¿Cuál es el mínimo número posible de fichas malas?
Solución:
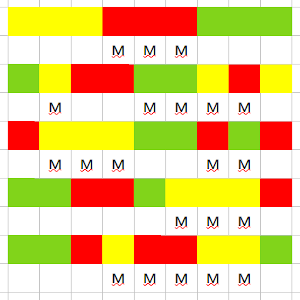
Como es lógico, debemos hacer un poco de experimentación, colocando una cantidad mucha menor de fichas. Como el tema va de paridad, empezaremos por probar series de 3 colores y 3 fichas de cada color, como indica el dibujo correspondiente.
Pronto podemos comprobar que resulta algo pesado contar el número de fichas de diferente color que hay antes y después, y que, puesto que el total de fichas es impar, es muy sencillo entender que en realidad es suficiente contar en un lado (al otro hay la misma paridad).
Si relacionamos las combinaciones con la paridad de la cantidad total de una ficha, resulta curioso comprobar que esta paridad coincide con la paridad entre fichas de un mismo color en el caso en que la ficha no sea mala, y es opuesta en el caso de que lo sea.
Es decir, voy a anotar la paridad de la cantidad de fichas que hay a la izquierda de una determinada, y también la paridad de fichas que hay a su izquierda del mismo color que la propia ficha.
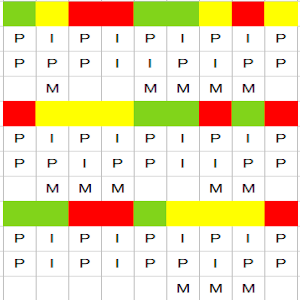
¿Por qué sucede esto? Porque la cantidad total de fichas antes de una coincide con la cantidad de fichas diferentes + la cantidad de fichas iguales.
En las fichas que no sean malas, la cantidad de fichas diferentes son pares, luego coincide la paridad de las cantidades totales y de las fichas iguales. Y en el caso de que sean fichas malas, serán justo de paridad contraria, ya que la suma de pares e impares siempre da impar, mientras que impares e impares da par.
La ventaja de anotar así las posiciones es que sabemos exactamente cuántas hay de cada tipo. Hay que observar que la paridad de las fichas que hay a la izquierda es alternante, y la cantidad de fichas del mismo color también lo es si nos fijamos sólo en las del mismo color.
Es decir, en nuestro ejemplo, siempre habrá dos fichas amarillas con una P y una con una I.
Por tanto, habrá en nuestro ejemplo, mirando la paridad del total de fichas a la izquierda, 5 P y 4 I. Mientras que mirando la paridad de fichas del mismo color, habrá 6P y 3I. Eso obliga a que haya un mínimo de una ficha mala, en la que no coincida una y otra paridad. Un ejemplo de esa distribución lo podemos ver a continuación.
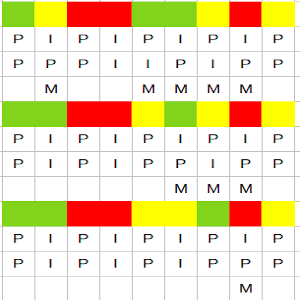
De hecho, lo hemos hecho cambiando pacientemente una casilla mala por otra para que coincidiesen en la medida de lo posible las I y las P.
Veamos cómo aplicarlo al caso de 2021 colores con 2021 fichas de cada color. En total, la secuencia de 2021² de fichas tendrán (2021² + 1)/2 posiciones P (con una cantidad par de fichas a su izquierda) y (2021² – 1)/2 posiciones I, ya que tenemos una P más una I y van en posiciones alternadas.
Ahora bien, en cada color hay 2021 fichas, por lo que si miramos si tienen una cantidad par o impar de su propio color, nos encontraremos que hay (2021 + 1)/2 P y (2021 – 1) I de cada color, es decir, en total habrá 2021(2021 + 1)/2 P y 2021(2021 – 1)/2 I.
Tenemos que comparar la diferencia entre los dos tipos de fichas P, es decir, hay que restar 2021(2021 + 1)/2 y (2021² + 1)/2.
Para ello, hacemos (2021² + 2021)/2 – (2021² + 1)/2 = (2021 – 1)/2 = 1010 fichas malas como mínimo, pues habrá 1010 P que no se podrán hacer coincidir con fichas P.
Para confirmar que es posible alcanzar este mínimo, podemos situar 2020 fichas de cada uno de los 2021 colores de forma consecutivas, lo que respetará la secuencia de par e impar en ambos recuentos, y dejar al final un total de 2021 fichas de todos los colores diferentes, que en el recuento de cuántas fichas de su color tienen a la izquierda siempre son P, y por tanto habrá un total de 1011 coincidencias y 1010 fichas en mala posición.
Con esto concluimos el apartado (a). Para el apartado (b), la cosa se complica, ya que si tenemos que situar las fichas en grupos de al menos 2 del mismo color, cada vez que situemos una con paridad diferente en cuanto a posición y color, las que le acompañen también serán malas.
Por otra parte, como de cada color hay una cantidad impar de fichas, al menos uno de las agrupaciones deberá ser de cantidad impar, al menos de 3.
Cuando usemos una agrupación impar se produce un desacoplamiento entre las dos paridades (de posición y de color) que sólo se puede compensar con otra agrupación impar.
Después de un desacoplamiento de ese tipo, todas las fichas que pongamos hasta que se compense serán malas, ya que no coincidirá su paridad de posición con su paridad de color.
Evidentemente, si queremos compensarla usando el menor número de fichas en mala posición, deberemos usar el impar más pequeño, es decir, el 3.
Y necesitaremos compensar al menos (2021 – 1)/2 = 1010 veces, es decir, que en el apartado (b) tendremos al menos 1010·3 = 3030 fichas malas.
Un ejemplo que prueba que esa situación es posible es situar, por ejemplo, 2021 fichas de un color, 3 de otra, 2021 de otra, y así sucesivamente hasta agotar los 2020 colores. Sólo las ternas de los colores separadores están en mala posición. Cuando situemos los 2020 colores, estaremos en condiciones de poner fichas de la misma paridad, así que pondremos las cantidades pares (2018 de cada color) de fichas que nos faltan por poner y las 2021 seguidas del último color. En total sólo hemos colocado 3·1010 = 3030 fichas malas.