Solución a “La familia Martínez”
Problema 1 del nivel B de la Olimpiada Provincial de Alicante de la Olimpiada de la Comunidad Valenciana de 2024 Se dirige a una edad de: 14 -15 años
Entre dos tenderos del Mercado Central de Alicante llevan al mercado 100 tomates.
Uno tiene más mercancía que el otro, pero ambos obtienen el mismo dinero al venderlo.
Si el primero los hubiese vendido al precio del segundo, habría ganado 45€, y si el segundo los hubiese vendido al precio del primero, habría ganado 20€. ¿Cuántos tomates tenía cada uno?

Solución:
(more…)La familia Martínez
Problema 1 del nivel B de la Olimpiada Provincial de Alicante de la Olimpiada de la Comunidad Valenciana de 2024 Se dirige a una edad de: 14 -15 años
Entre dos tenderos del Mercado Central de Alicante llevan al mercado 100 tomates.
Uno tiene más mercancía que el otro, pero ambos obtienen el mismo dinero al venderlo.
Si el primero los hubiese vendido al precio del segundo, habría ganado 45€, y si el segundo los hubiese vendido al precio del primero, habría ganado 20€. ¿Cuántos tomates tenía cada uno?

Solución: Aquí.
Solución a “Deporte optativo”
Problema 1 del nivel A de la Olimpiada Provincial de Alicante de la Olimpiada de la Comunidad Valenciana de 2024 Se dirige a una edad de: 12 -13 años
En una clase de segundo de ESO algunas personas juegan al voleibol y todas las demás juegan al fútbol.
En total, el número de chicas que practican fútbol, junto a los chicos que practican voleibol, son 16.
Hay 11 personas que practican fútbol.
Hay 10 chicas en la clase.
El total de chicas que practican voleibol junto al total de chicos es 16.

Solución:
(more…)Deporte optativo
Problema 1 del nivel A de la Olimpiada Provincial de Alicante de la Olimpiada de la Comunidad Valenciana de 2024 Se dirige a una edad de: 12 -13 años
En una clase de segundo de ESO algunas personas juegan al voleibol y todas las demás juegan al fútbol.
En total, el número de chicas que practican fútbol, junto a los chicos que practican voleibol, son 16.
Hay 11 personas que practican fútbol.
Hay 10 chicas en la clase.
El total de chicas que practican voleibol junto al total de chicos es 16.

Solución: Aquí.
Solución a “Juego de cifras”
Problema 1 del nivel C de la Olimpiada Provincial de Alicante de la Olimpiada de la Comunidad Valenciana de 2024 Se dirige a una edad de: 10 -11 años
Haciendo uso de las cuatro operaciones básicas (suma, resta, multiplicación y división), intenta conseguir el número 721 usando los números siguientes una única vez: 75, 6, 1, 2, 10, 7.
(Hay más de una solución, cuantas más consigas, mejor puntuación tendrás en este problema. Las operaciones se pueden repetir).

Solución:
El número de posibles operaciones que puedes llevar a cabo es realmente grande y ni siquiera con un ordenador sería un problema sencillo.
(more…)Juego de cifras
Problema 1 del nivel C de la Olimpiada Provincial de Alicante de la Olimpiada de la Comunidad Valenciana de 2024 Se dirige a una edad de: 10 -11 años
Haciendo uso de las cuatro operaciones básicas (suma, resta, multiplicación y división), intenta conseguir el número 721 usando los números siguientes una única vez: 75, 6, 1, 2, 10, 7.
(Hay más de una solución, cuantas más consigas, mejor puntuación tendrás en este problema. Las operaciones se pueden repetir).

Solución: Aquí.
Solución a “Capicúa”
Problema 3 del concurso Marató de problemes 2024 Se dirige a una edad de: 14-15 años
Ariadna ha de sumar el conjunto de los 125 números capicúas de 5 cifras en los que todas y cada una de las cifras que los forman son impares.
Sin embargo, a la hora de calcular la suma se ha dejado uno de los números y sólo ha sumado 124.
Ha obtenido el número 6 913 262.
¿Cuál es el número que no ha sumado?
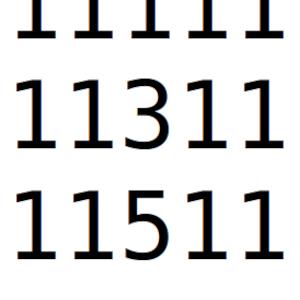
Solución:
(more…)
Capicúa
Problema 3 del concurso Marató de problemes 2024 Se dirige a una edad de: 14-15 años
Ariadna ha de sumar el conjunto de los 125 números capicúas de 5 cifras en los que todas y cada una de las cifras que los forman son impares.
Sin embargo, a la hora de calcular la suma se ha dejado uno de los números y sólo ha sumado 124.
Ha obtenido el número 6 913 262.
¿Cuál es el número que no ha sumado?
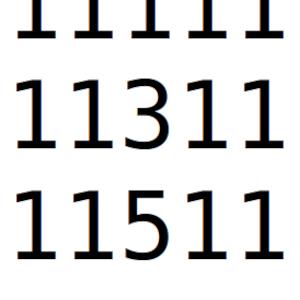
Solución: Aquí.
Solución a “De hexágono a triángulo”
Problema 2 del concurso Marató de problemes 2024 Se dirige a una edad de: 14-15 años
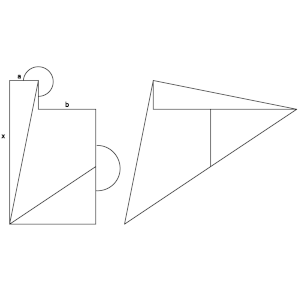
El hexágono de la izquierda tiene todos los ángulos rectos, y las longitudes de dos lados son a y b, tal y como está indicado en la figura.
Si dividimos el hexágono en las tres partes que muestra la figura y las giramos adecuadamente, podemos componer un triángulo.
Expresa la longitud x, que corresponde al lado izquierdo del polígono inicial, en función de a y b.
(Por si es demasiado pequeño, aclaro que a y b son las longitudes de los dos lados horizontales superiores del hexágono.)
Solución:
(more…)
De hexágono a triángulo
Problema 2 del concurso Marató de problemes 2024 Se dirige a una edad de: 14-15 años
El hexágono de la izquierda tiene todos los ángulos rectos, y las longitudes de dos lados son a y b, tal y como está indicado en la figura.
Si dividimos el hexágono en las tres partes que muestra la figura y las giramos adecuadamente, podemos componer un triángulo.
Expresa la longitud x, que corresponde al lado izquierdo del polígono inicial, en función de a y b.
(Por si es demasiado pequeño, aclaro que a y b son las longitudes de los dos lados horizontales superiores del hexágono.)

Solución: Aquí.