Problema 7 del concurso Marató de problemes 2022
Se dirige a una edad de: 14-15 años

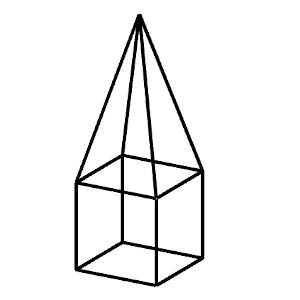
Una pirámide recta de h centímetros de altura tiene como base una de las caras de un cubo.

La suma de las longitudes de las aristas de la pirámide es igual a la suma de las longitudes de todas las aristas del cubo.

¿Cuál es el área de la base de la pirámide? (Se debe dar en función de h)

Solución:

Llamemos 2x al lado del cubo, que también es lado de la base de la pirámide (para no estar trabajando todo el rato con fracciones).

Las aristas del cubo son todas iguales y miden en total 24x en longitud.

Puesto que la pirámide es recta y tiene una altura de h, las aristas de la pirámide que no están en la base tienen, cada una de ellas, una longitud de raíz(h² + x² + x²), ya que son la diagonal de un paralelepípedo que tiene una longitud h y dos longitudes x.

En total, la pirámide tiene 4 lados de longitud 2x, y otros 4 de longitud raíz(h² + 2x²).

Puesto que miden lo mismo, tenemos que 24x = 8x + 4raíz(h² + 2x²), de donde raíz(h² + 2x²) = 4x.

Elevando al cuadrado, tenemos que h² + 2x² = 16x², por lo que h² = 14x². Por eso, x² = h²/14.

Puesto que el área de la base de la pirámide es 4x², eso corresponde a 2h²/7.

Otra manera de abordar este trabajo es fijar un parámetro y calcular la h para un valor determinado del lado de la base (por ejemplo, 2 cm, ya que hay que dividirla entre 2 para encontrar el centro del lado, y por tanto calcular la altura de la pirámide). Una vez conocida esta altura para un valor 2 (que sería 2·raíz(14) o raíz(56)) se determinaría de forma proporcional al valor h el valor del lado, lo que permitiría calcular el área que buscamos, que sería el lado al cuadrado.