Problema 2 de la Olimpiada Matemática Femenina Europea (EGMO 2018) Se dirige a una edad de: 17 años
Considere el conjunto A = {1 + 1/k / k = 1, 2, 3,…}.
a) Demuestre que todo entero x ≥ 2 puede ser escrito como producto de uno o más elementos de A, no necesariamente distintos.
b) Para todo entero x ≥ 2, sea f(x) el menor entero tal que x puede ser escrito como f(x) elementos de A, no necesariamente distintos.
Demuestre que existen infinitos pares (x, y) de enteros, con x ≥ 2, y ≥ 2, tales que f(xy) < f(x) + f(y).
Nota: los pares (x, y), (z, t) son diferentes si x es diferente de z o y es diferente de t.
 Solución:
Solución:
En este caso, deberemos trabajar practicando con el conjunto, que estará formado por los números 2, 3/2, 4/3, 5/4, 6/5, etc. Es sencillo observar que todos los números del conjunto son más pequeños que el primero, más pequeños que 2.
Para resolver el apartado (a), tratamos de conseguir los primeros números, hasta conseguir obtener un patrón. Por ejemplo, 2 es un elemento del conjunto, por lo que para x = 2 es evidente. El número 3 se puede conseguir como 3/2·2, y el 4 como 2·2, y el 5 como 5/4·2·2.
Formar un número genérico x como producto de x/(x – 1)·(x – 1)/(x – 2)·…·2/1 es muy sencillo, ya que cada elemento del conjunto tiene como denominador el numerador del anterior, y al multiplicar todos los elementos entre sí se anularán. Pero puede que existan productos de menos factores que produzcan el mismo resultado.
El apartado (b) es mucho más difícil de lograr. Para estudiar un poco los valores y las propiedades de la función f que se define en este apartado, la estudiaremos en los casos más pequeños.
Preparamos una colección detallada.
Evidentemente, f(2) = 1, f(3) =2. También f(4) = 2, ya que 4 = 2·2.
Ver que f(5) = 3 es más complicado, ya que sólo 2 tiene f(2) = 1, y necesitas un número mayor que 2 para obtener un factor 5 en el numerador en un producto de elementos de A. Y 5 = 5/4·2·2.
De nuevo, f(6) = 3 (6 = 3/2·2·2) y es el resultado mejor.
A partir de aquí, podemos observar que es mejor pensar al contrario, obtener todos los productos enteros de n elementos de A, y así obtendremos los enteros x tales que f(x) = n.
Con un único factor sólo tenemos el 2 (por eso f(2) = 1).
Con dos factores, tenemos 3/2·2 = 3 y 2·2 = 4 (f(3) = 2, f(4) = 2).
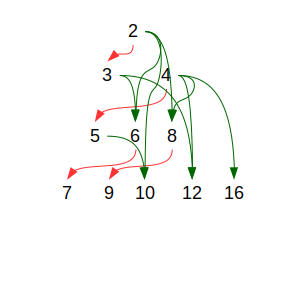
Con tres factores, tenemos 3/2·2·2 = 6, 2·2·2 = 8, 4/3·3/2·2 = 4 (ya estaba), y 5/4·2·2 = 5, luego f(6) = f(8) = f(5) = 3.
Con cuatro factores (eliminando los ya obtenidos), tenemos 7 = 7/6·3/2·2·2, 12 = 3/2·2·2·2, 9 = 9/8·2·2·2, 16 = 2·2·2·2 y 10 = 5/4·2·2·2, luego f(7) = f(12) = f(9) = f(16) = f(10) = 4.
Claro, que cada paso obtenemos los siguientes de los que ya teníamos (usando la fracción correspondiente de A), y los posibles productos de dos cuyas f sumen el número adecuado, siempre que no los hubiésemos obtenido antes. Así, sumando 1 (usando una fracción de A), obtenemos que 5 = f(11) = f(13) = f(17). Multiplicando uno de aquellos en los que f vale 4 con 2, que es el único en el que f vale 1, 5 = f(14) = f(18) = f(20) = f(24) = f(32), mientras que 5 = f(15), ya que es producto de 3 (f(3) = 2) por 5 (f(5) = 3).
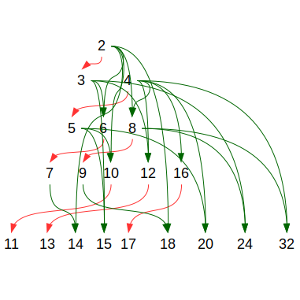
Tened paciencia para obtener los números. Por ejemplo, 17 = 17/16·2·2·2·2, y 15 = 5/4·3/2·2·2·2, mientras que 13 = 13/12·3/2·2·2·2.
Hemos encontrado un patrón, aunque puede que no esté muy claro.
Factorizando, encontramos que aún se cumple que f(xy) = f(x) + f(y) para todos los valores que tenemos hasta ahora, necesitamos subir a un valor algo mayor para que esto cambie, como nos proponen que pase.
Entre los elementos que dan un valor 6 para f, tenemos a 19, 21, 25 y 33, a través de fracciones del conjunto multiplicadas por elementos de valor 5, 22, 26, 28, 34, 40, 48 y 64, multiplicando 2 por elementos de valor 5, y 30 y 27, que se pueden obtener multiplicando 3 por elementos de valor 4. Todos ellos, puesto que no se han podido conseguir con menos productos, tienen un valor f de 6.
Aquí encontramos una pareja de números que cumplen lo que nos piden. f(3·11) = f(33) = 6 < f(x) + f(y) = 2 + 5, según hemos razonado. Ya tenemos uno de los valores que cumple que f(xy) < f(x) + f(y).
Veamos el razonamiento general. Tomemos un número p cualquiera. Supongamos que las tres igualdades siguientes son ciertas: f(p·33) = f(p) + f(33), f(p·33) = f(3) + f(p·11) y f(p·11) = f(11) + f(p). Entonces f(p·33) = f(3) + f(11·p) = f(3) + f(11) + f(p), que sabemos que es menor que f(33) + f(p) = f(p·33). Luego llegamos a una contradicción, por lo que una de las igualdades anteriores no es cierta, y por lo tanto se da que, o bien f(p·33) < f(p) + f(33), o bien f(p·33) < f(3) + f(p·11), o bien f(p·11) < f(11) + f(p).
Utilizando valores sucesivos de p que proporcionen números cada vez mayores, podemos lograr infinitas desigualdades como la solicitada. Dicho de otro modo, si el conjunto de valores en los que se cumple la desigualdad fuera finito, habría un valor p que sería cota superior del conjunto de los productos, y usando ese número, obtendríamos uno de los valores anteriores, que todos ellos estarían por encima del valor p (tanto 33p, como 11p).
Otra forma de abordar el problema es buscar familias de elementos concretas que sea relativamente sencillo probar que no cumplen la igualdad. Las soluciones oficiales juegan con números de la forma 5 y (2^(4k + 2) + 1)/5, pero también es muy farragoso probar que efectivamente se cumple la desigualdad, aunque es sabido que infinitas potencias de 2 acaban en 4, y sumándole 1, por tanto, serían divisibles entre 5. Otro camino por el que encontrar números concretos propuesto puede ser usar 2^k + 1 y 4^k – 2^k + 1, pero tampoco veo sencillo encontrar esta situación clara.