Problema 3 de la Olitele (Olimpiada Telemática de Cataluña) 2017
Se dirige a una edad de: 16-17 años

Un número de tres cifras que son todas diferentes de cero es un cuadrado perfecto.

Si escribimos el número con las cifras en orden inverso, obtenemos un número menor que el inicial.

Si los restamos obtenemos un número múltiplo de 8.

¿Cuál es el número de tres cifras que teníamos al principio?

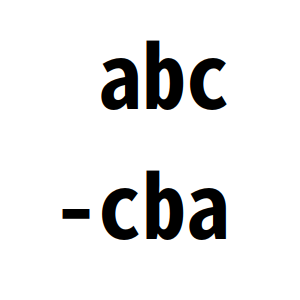
Solución:

Sólo hay 21 cuadrados perfectos entre 111 y 999, de forma que es factible tratar de calcularlo por ensayo y error, pero vamos a tratar de convertir este ejercicio en algo más algebraico.

La representación decimal de un número que tenga las cifras a b y c sería 100a + 10b + c. Si invertimos esas cifras, tendremos 100c + 10b + a. La diferencia, por tanto, sería 99a – 99c = 99(a – c) (recuerda que la versión invertida es menor).

Es decir, que la diferencia siempre es múltiplo de 99. Eso significa que, para ser múltiplo de 8, el otro factor deberá serlo, de forma que, o bien a = c (pero en este caso invertir las cifras no daría un número inferior), o bien a – c = 8. Sin embargo, puesto que son cifras, sólo puede darse el caso de que a = 8 y c =0, o bien a = 9 y c = 1. Pero c no puede anularse, por lo que se trata de a = 9 y c = 1.

Es decir, nos quedan muchas menos posibilidades, ya que 30·30 = 900, sólo puede tratarse de 31·31 = 961.

En efecto, 961 es un cuadrado perfecto y 961 – 169 = 792 = 99·8, es evidentemente un múltiplo de 8.