Problema 9 de la Olitele (Olimpiada Telemática de Cataluña) 2017
Se dirige a una edad de: 16-17 años

Sabemos que x e y son dos números positivos, de forma que x es mayor que y y cumplen las dos relaciones siguientes para dos números racionales concretos A y B:

(x + y)(x² – y²) = A

(x – y)(x² + y²) = B

Calcula el valor de x/y.

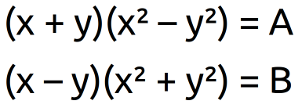
Solución:

Está claro que en la primera ecuación podemos factorizar, de forma que (x + y)²(x – y) = A. Así, ambas ecuaciones quedan con un factor positivo (x – y), de forma que al dividir ambos extremos de la igualdad, quedaría (x + y)²/(x² + y²) = A/B.

Como buscamos x/y, dividiendo en el denominador y el numerador de la primera fracción por y² queda una expresión que sólo depende de x/y, (x/y + 1)²/(x²/y² + 1) = A/B.

Transformando z = x/y, tenemos que (z + 1)²/(z² + 1) = A/B.

Si has tenido dificultades con esta simplificación, también es posible sustituir x = z·y, y extraer y simplificar el factor y². Ten en cuenta al dividir por y² que, como en el numerador hay dos factores, cada uno queda dividido por una y, mientras que ambos sumandos del denominador se dividen por y².

Ahora, reducimos a común denominador y eliminamos este denominador, de forma que tenemos la expresión (z + 1)²B = (z² + 1)A, y desarrollando, queda la ecuación Bz² + 2Bz + B = Az² + A, que recuerda a una ecuación de segundo grado en z.

Volvamos al primer párrafo. Como x e y son números positivos, (x + y)² es algo mayor que x² + y², así que A es mayor que B. Por lo tanto, restaremos la parte donde hay B, y tenemos que la ecuación queda 0 = (A – B)z² – 2Bz + (A – B). Como aparece dos veces el coeficiente A – B, podemos dividir por él, quedando 0 = z² – 2B/(A – B)z + 1.

Por tanto, las dos soluciones de la ecuación podrán ser respuestas al valor de x/y, siempre y cuando se trate de números mayores que 1. De momento, llamaremos q a B/(A – B) para abreviar.

La expresión de z será z = (2q + raíz(4q² – 4) )/2 = q + raíz(q² – 1), mientras que la otra solución sería z = q – raíz(q² – 1).

Hay que tener en cuenta que q debe ser mayor que 1 para que se puedan dar las igualdades (en caso contrario, no existirá ningún valor de z), y que, en ese caso, es sencillo ver que la segunda de las posibilidades es menor que 1, de forma que sólo hay un valor, la suma (por ejemplo, podemos poner q = s – 1, y escribir la fórmula, comprobando que realmente queda menor que 1).

Si queremos expresar x/y sólo en función de A y B, sustituimos en la fórmula y ponemos denominador común, consiguiendo la igualdad siguiente: x/y = (B + raíz(2AB – A²))/(B – A).

Como se supone que al concursante se le da el valor concreto de A y de B, es sencillo hacer el cálculo.