Problema 6 de la Fase Local (sábado) de la Olimpiada Matemática Española (2018) Se dirige a una edad de: 16-17 años
Se han coloreado 46 cuadrados unitarios de una cuadrícula 9×9.
¿Hay, en la cuadrícula alguna figura compuesta de tres cuadrados formando esquina en cualquier orientación, como en el dibujo que acompaña estas líneas, con las tres casillas coloreadas?
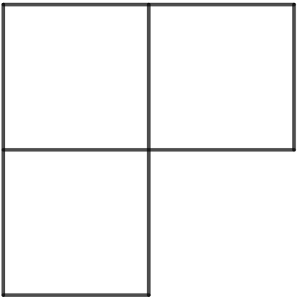
Solución:
Observa que si pidiesen algo parecido con 45, sería fácil encontrar una coloración en la que no se diese tal situación, pintando cinco de las nueve líneas y dejando cuatro intercaladas sin colorear.
En el fondo, nos están pidiendo que coloreemos un cuadrado más de lo que son más de la mitad de líneas, y que comprobemos que siempre hay un dibujo del tipo que nos piden.
El equivalente en un cuadrado 3×3 sería pintar 7 cuadrados, y en un 5×5, pintar 16. después de ensayar en tableros pequeños, podemos llegar a conclusiones interesantes.
Por ejemplo, en un cuadrado 2×2, pintar dos es posible sin que aparezca esta figura, pero pintar más de 2 no.
Si tratamos de hacer algo similar en uno 3×3, aparece una figura como la siguiente, en la que hay dos zonas, una verde y una azul. Si pintamos dos de la zona verde no aparece ningún dibujo del tipo que nos piden, y podemos pintar cuatro de la zona azul sin que tampoco aparezcan (tres en línea y uno separado de esa línea). En total, hay un máximo de 6 cuadrados que podemos pintar sin que aparezca el cuadrado. Tratar de colorear siete conlleva, por tanto, que o bien pintamos tres de la zona verde, o los cinco de la zona azul, por lo que aparece seguro una figura en el tablero de la forma que buscamos. La única forma de pintar 6 es mediante el dibujo de dos franjas de 3 separadas por una franja de 3 sin pintar.
El razonamiento en el tablero grande, puede ser delimitar zonas en la cuadrícula 9×9 que nos permita poner un tope de cuadrados por zona para pintar. Es evidente que 16 de esas zonas podrían ser cuadrados 2×2, pero el resto deben tener otra forma.
He probado a hacerlas rectas, o mediante cuadrados 3×3, pero el razonamiento se complica mucho. De esta forma, al rellenar cuadrados de una línea, si son cuadrados consecutivos, pueden obligar a las zonas 2×2 a seguir un determinado patrón, pero no es fácil seguir el razonamiento y no me ha resultado cómodo escribirlo hasta el final. Sospecho que se podría concluir.
La otra forma, que es la que propone la solución oficial, es encajar los 16 cuadrados 2×2 dejando lo más parecido a una diagonal, y dividir la diagonal de otra forma.
Así, encontramos una disposición en forma de 16 cuadrados, tres figuras de cuatro cuadrados en forma de letra l, y una figura de cinco cuadrados similar a la zona azul de la cuadrícula 3×3, como una letra l mayúscula.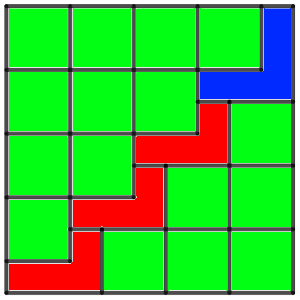
El máximo de cuadrados que podemos pintar de esas zonas (sin que aparezca la figura que hemos descrito al principio del problema) sería, por tanto, 2 por cada una de los cuadrados 2×2, con un total de 16·2 = 32, tres de las zonas en forma de letra l de cuatro cuadrados (un máximo de 3·3 = 9), y hasta cuatro de la zona de cinco cuadrados con forma de letra l mayúscula. Eso haría que el máximo de cuadrados que podemos colorear sin que aparezca una figura del tipo que se nos pide es de 32 + 9 + 4 = 45.
Por lo tanto, pintar 46 implica rellenar totalmente una de las cinco zonas de la diagonal (con lo que aparece una figura de las pedidas), o bien pintar tres de los cuatro cuadrados de una de las zonas 2×2, con lo que seguro que podríamos encontrar una figura del tipo que nos piden.