Problema 1 de la Olimpiada Internacional (2018) Se dirige a una edad de: 17-19 años
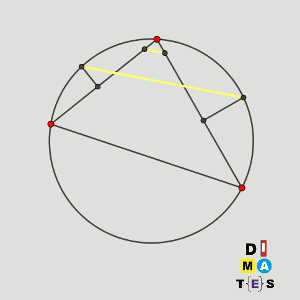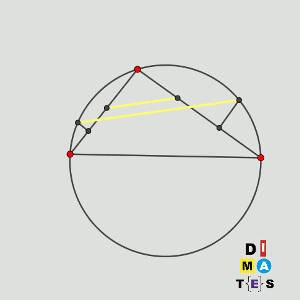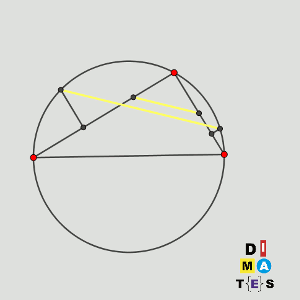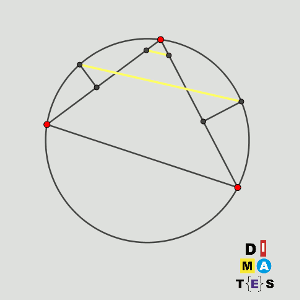
Sea P la circunferencia circunscrita al triángulo acutángulo ABC. Los puntos D y E están en los segmentos AB y AC, respectivamente, y son tales que AD = AE. Las mediatrices de BD y CE cortan a los arcos menores AB y AC de P en los puntos F y G, respectivamente.
Demostrar que las rectas DE y FG son paralelas (o son la misma recta).
Solución:
Se trata de un problema realmente difícil, para mi gusto. La construcción no es muy complicada, pero el resultado no es inmediato.
Hay varias formas de probarlo, incluso una algebraica usando números complejos, pero como es un problema de geometría, vamos a tratar de resolverlo con resultados geométricos conocidos.
Lo más elemental del dibujo es que, por estar a la misma distancia E y D de A, están sobre otra circunferencia de centro A. La intersección de ambas circunferencias tiene una curiosa propiedad, en este contexto.
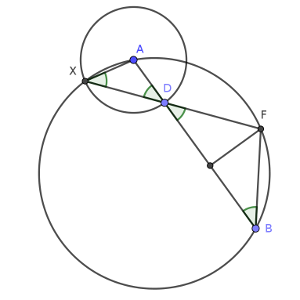
Debemos observar que, cuando trazamos la mediatriz, todos los puntos, incluido el F, están a la misma distancia de B y de D. y por tanto, los dos ángulos FDB y FBD son iguales. Pero, claro, en la otra circunferencia, AD es un radio, mide lo mismo que AX, por lo que AXD forma un triángulo isósceles, y el ángulo AXD mide también lo mismo que ADX. Como X es un punto de la circunferencia P que forma ángulo entre A y F, al igual que B, resulta que los cuatro ángulos son iguales. Es decir, que la linea que une F con D pasa por la intersección de las dos circunferencias, igual que la linea que une G con E por la otra intersección.
El dibujo, entonces, se puede ver de otra forma, si incluimos las dos intersecciones (X e Y).
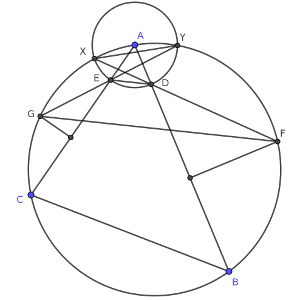
Ahora, el ángulo XDE es el mismo, por estar en la circunferencia de centro A, que el XYE, que es el XYG, y que es el mismo que XFG, por estar Y y F en la misma circunferencia P.
Como el ángulo XDE es el mismo que XFG, los segmentos DE y FG son paralelos, como se quería demostrar.
Nuestro amigo Ignacio Larrosa nos ha hecho un applet de Geogebra. En él puedes modificar la posición de los puntos y verificar que se sigue cumpliendo. ¡Muchas gracias!
¿Por qué acutángulo? De hecho en la animación, la mitad del tiempo es obtusángulo. por otra parte, un pequeño ‘gazapo’: El triángulo AXD es isósceles, no tiene que ser equilátero.
Pero no parece muy complicado para una Olímpiada internacional, ¿no?
Ahora mismo corrijo, se les habrá pasado a mis correctores.
Es el más sencillo de la IMO. Lo ha resuelto la mayoría de participantes. Por eso hay tanta mención honorífica.
No es “demasiado fácil”, suele haber uno al menos de este nivel. Ten en cuenta que no puedes poner todos del nivel del 6, sería imposible hacer distinciones entre unos y otros (habría un 95% de ceros).
No entiendo por qué se exige que sea acutángulo. Está en el enunciado, pero me da la sensación de que no es necesario realmente.