Problema 4 de la Olimpiada Internacional (2018) Se dirige a una edad de: 17-19 años
Un lugar es un punto (x, y) en el plano tal que x e y son ambos enteros positivos menores o iguales que 20.
Al comienzo, cada uno de los 400 lugares está vacío.
Ana y Beto colocan piedras alternadamente, comenzando por Ana. En su turno, Ana coloca una nueva piedra roja en un lugar vacío tal que su distancia entre cualesquiera dos lugares ocupados por una piedra roja es distinto de la raíz de 5.
En su turno, Beto coloca una nueva piedra azul en cualquier lugar vacío (un lugar ocupado por una piedra azul puede estar a cualquier distancia de cualquier otro lugar ocupado).
Ellos paran cuando alguno de los dos no pueda colocar una piedra.
Halla el mayor k tal que Ana pueda asegurarse de colocar al menos K piedras rojas, sin importar cómo Beto coloque sus piedras azules.

Solución:
Otro problema digno de Olimpiada Internacional. Da mucho que pensar, aunque no es de dificultad excesivamente elevada. En este problema hemos iniciado una sección de encuestas en las que puedes dejar tu opinión sobre la dificultad.
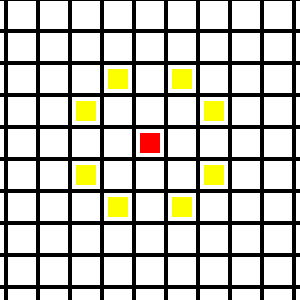
Lo primero que debemos hacer, puesto que estamos más familiarizados, es transformar nuestra red de lugares en un tablero cuadrado de 20×20 casillas. En ese caso, los jugadores irán poniendo fichas rojas y azules, y la dificultad relacionada con las distancias consiste en que no podemos situar dos fichas rojas de forma que el vector (2, 1) o el (1, 2), o cualquiera con los mismos valores absolutos transforme un punto en el otro. En nuestro tablero, de una ficha roja a otra no debemos poder pasar con un movimiento de caballo de ajedrez. Ésto es debido a que la distancia raíz de 5 sólo se puede conseguir si la suma de las variaciones de la posición horizontal y de la vertical al cuadrado da 5, y la única forma de conseguir un 5 sumando dos cuadrados enteros es usando un dos (o un menos dos) y un uno (o un menos uno).
En definitiva, que cada vez que Ana ponga una ficha, estará bloqueando (no podrá usar) entre dos y ocho casillas, como está representado en la siguiente imagen.
Ahora, conviene ensayar con tableros pequeños. Primero, a jugar como si Beto no existiese, y después, introduciendo un Beto que trate de bloquear posiciones para Ana.
El tablero más ilustrativo, es el de 4×4, ya que es par, como nuestro ejemplo, y suficientemente grande como para hacer movimientos de caballo.
Cada vez que Ana sitúa una ficha, bloquea varias posiciones, por lo que debería situarla de forma que sólo bloquee casillas ya bloqueadas, para que pueda poner una cantidad grande de fichas. Pensando en un tablero ajedrezado, cada vez que sitúa sus fichas sobre casillas de un color, bloquea casillas de color contrario, así que parece lógico que siempre sitúe sus fichas sobre un mismo color.
Por lo tanto, si juega sola en un tablero 4×4, podrá situar un máximo de 8 fichas, cuidando de escoger sólo casillas blancas o negras.
Si juega con Beto, y Beto se da cuenta de esa estrategia, puede ir tapando casillas de ese mismo color, según haya escogido Ana inicialmente, para impedirle colocar la mitad de esas fichas, hasta un máximo de 4.
Si Ana no juega con esa estrategia, cada vez que sitúe una ficha, bloqueará más de las que ponga (cada ficha bloquea dos casillas, por lo menos), y podría situar menos de la tercera parte de las disponibles. Como además, Beto puede tratar de tapar casillas ventajosas desde el punto de vista de Ana, Ana no obtendría más fichas puestas de las 4 que hemos estudiado.
Así, Cada movimiento de Ana, Beto debe estudiar qué casillas han quedado bloqueadas, y desde qué casillas se bloquean las mismas (que, normalmente, tendrán el mismo color que donde ha puesto Ana), situando su ficha en una de ellas. Y, por tanto Ana puede colocar 4 fichas haga lo que haga Beto, y no más.
A continuación, expongo una animación en la que se estudia una partida de este tipo.

El tablero de 20×20 es un tablero que contiene 25 tableros 4×4. Si Beto juega de la misma forma que hemos descrito en cada uno de ellos (siempre en el mismo que juegue Ana), en cada uno de los 25 Ana no podrá situar más de 4, por lo que k vale 100 = 25×4, y Beto podrá impedir que ponga una más. Y podrá situarlas siempre, si recurre a casillas en diagonal (que tengan el mismo color).
Por favor, danos tu opinión sobre la dificultad de este problema en la encuesta siguiente.
[polldaddy poll=10082460]