Problema 2 del viernes de la Fase Local de la LV OME 2019
Se dirige a una edad de: 16-17 años

Demuestra que para todo n ≥ 2 podemos encontrar n números reales x₁, x₂, …, x_n ≠ 1 de manera que los productos x₁·x₂·…·x_n y (1/(1 – x₁))·(1/(1 – x₂))·…·(1/(1 – x_n)) son iguales.

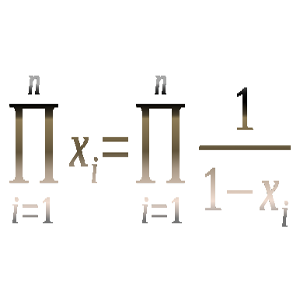
Solución:

Vamos con uno de los problemas que decide más de la Fase Local.

Debemos empezar estudiando el caso para n = 2 (es sencillo ver que para n = 1 no existe un número en el que la igualdad se dé, pero eso no parece tener consecuencias para el problema).

Para buscar los dos números, podemos recurrir a fijar uno de los números y buscar el otro. Por ejemplo, si uno de los números vale 2, tenemos la ecuación 2·x = 1/(1 – 2)·1/(1 – x), que se transforma quitando denominadores en –2x(1 – x) = 1. Quitando los paréntesis y transformando un poco, tenemos que 2x² – 2x – 1 = 0, lo que proporciona una ecuación de segundo grado que tiene dos soluciones. Cualquiera de ellas nos vale como segundo número, por ejemplo (1 + raíz(3))/2.

En efecto, veamos que el par de números 2, (1 + raíz(3))/2 vale. El producto de ambos es 1 + raíz(3). Por otra parte, 1 – 2 = -1, y 1 – (1 + raíz(3))/2 = (2 – 1 – raíz(3))/2 = (1 – raíz(3))/2. Ahora, si invertimos estos números y los multiplicamos, da 1/(-1)·1/((1 – raíz(3))/2) = 2/(raíz(3) – 1) y este número, racionalizando, es decir, multiplicando numerador y denominador por (raíz(3) + 1), da 2·(raíz(3) + 1)/(3 – 1) = raíz(3) + 1. Otra forma de ver que ambos resultados son iguales es reduciéndolos al mismo denominador, donde vemos que sale el mismo numerador también.

En general, poniendo cualquier número como número inicial funciona, incluso se puede hacer en general.

Para tres números podemos intentar el mismo proceso, pero hay que elegir cuidadosamente los números. Por ejemplo, si usamos 2 y 2 como dos números iniciales (una de las claves es que se puede repetir), la ecuación queda 4x = 1/x, de donde obtenemos un valor x = 1/2 de forma muy sencilla. Está claro que 2·2·1/2 = (-1)·(-1)·1/(-1/2).

Y a partir de aquí, tenemos una manera de acelerar mucho el proceso, ya que podemos encontrar cuatro números sencillamente repitiendo los dos primeros (si funciona con dos, funciona con cuatro), y cinco repitiendo los dos primeros y los tres segundos, y así sucesivamente.

Por tanto, por inducción, si suponemos que n > 3, puesto que existe una cadena de n – 2, añadimos a ésta los dos que hemos encontrado en el paso n = 2. Y así se prueba la existencia de una sucesión.