Problema 3 del viernes de la Fase Local de la LV OME 2019 Se dirige a una edad de: 16-17 años
El trapecio isósceles ABCD tiene lados paralelos AB y CD. Sabemos que AB = 6, AD = 5 y el ángulo DAB = 60º. Se lanza un rayo de luz desde A que rebota en CB en el punto E e interseca en AD en el punto F. Si AF = 3, calcula el área del triángulo AFE.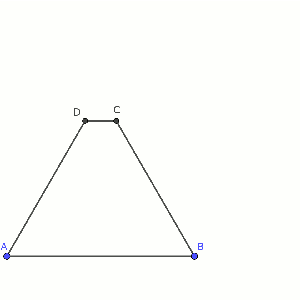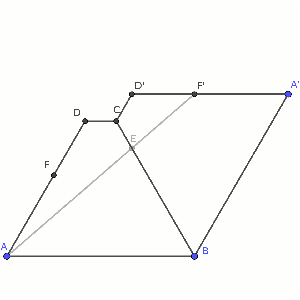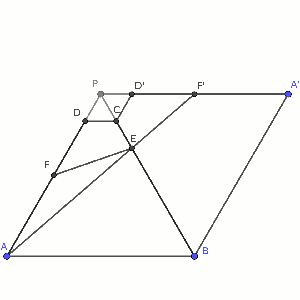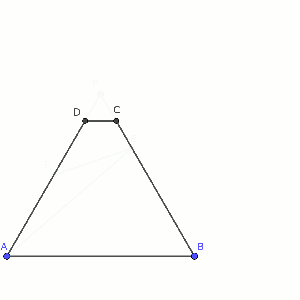
Solución:
No es fácil dibujar este tipo de situaciones, aunque abundan en los planteamientos de problemas. Para dibujar una reflexión o un rebote, es conveniente pensar que el rayo reflejado sigue recto al otro lado del espejo, o que la bola que rebota sigue recto, continuando por una figura simétrica a la original a lo largo de esa línea.
Por eso, como podéis ver en la animación que acompaña a este artículo, la forma de dibujarlo es hacer una simetría del trapecio, y trazar una línea recta, y luego trazar la línea que sigue el verdadero reflejo.
El caso es que una vez que tenemos la imagen clara dibujada, pensar en ángulos. Puesto que tenemos ángulos de 60º es sencillo completar el dibujo hasta rodearlo de un triángulo equilátero, y se aprecia una gran semejanza entre los triángulos ABE y FPE (claramente, tienen el mismo ángulo en E, por reflexión, y en B y en P, por tratarse de un triángulo equilátero).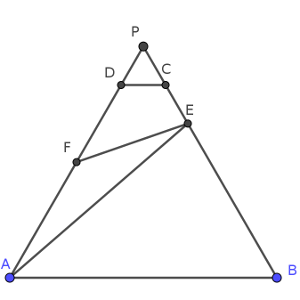
Como conocemos la distancia de AB, que vale 6, y podemos deducir la distancia FP (como la distancia AF es 3, FP vale 3 también), sabemos que la escala entre ambos triángulos es 2. Llamando x a la distancia BE, e y a la distancia EP, tenemos que x = 2y, y x + y = 6, con lo que 3y = 6, es decir, y = 2, x = 4. Así que BE vale 4, y EP vale 2.
Ahora estamos preparados para calcular el área de AEF, ya que sería el área de todo el triángulo equilátero menos la suma de las áreas de ABE y FPE.
Para calcular el área de un triángulo equilátero, podemos, por ejemplo, calcular su altura, dividiéndolo en dos triángulos rectángulos iguales. Razonando por trigonometría, su altura al cuadrado deberá valer 36 – 9 = 27. Es decir, que la altura debe valer raíz(27) = 3·raíz(3).
El área del triángulo equilátero de lado 6 será (6·3·raíz(3))/2 = 9·raíz(3).
Ahora, en el triángulo ABE tendrá una base 6, pero puesto que contiene un triángulo equilátero de lado 4, su altura estará dividida por la escala 6/4, es decir, que la altura valdrá 4·3·raíz(3)/6 = 2·raíz(3), y su área será 6·2·raíz(3)/2 = 6·raíz(3).
Y el triángulo FPE, si lo apoyamos sobre la base PE, que tiene 3 unidades, contiene una altura que coincide con la de un triángulo equilátero de lado 2, que será raíz(3), así que su área será 3·raíz(3)/2.
Por tanto, la suma de áreas de ABE y FPE tendrá un valor de 15·raíz(3)/2, y si lo restamos de 9·raíz(3), tendremos que el área de AFE, que era lo que nos pedían, será 3·raíz(3)/2.