Problema 4 del viernes de la Fase Local de la LV OME 2019 Se dirige a una edad de: 16-17 años
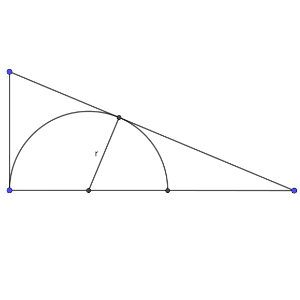
Sea p ≥ 3 un número primo, y consideremos el triángulo rectángulo de cateto mayor p² – 1 y cateto menor 2p.
Inscribimos en el triángulo un semicírculo cuyo diámetro se apoya en el cateto mayor y es tangente a la hipotenusa y al cateto menor del triángulo.
Encuentra los valores de p para los cuales el radio del semicírculo es un número entero.
Solución:
Calcular las medidas del triángulo rectángulo es sencillo, ya que ( p² – 1)² + (2p)² = p⁴ – 2p² + 1 + 4p² = p⁴ + 2p² + 1 = (p² + 1)², así que la hipotenusa mide p² + 1.
Podemos tomar un par de ejemplos para trabajar con el problema (el menor sería p = 3, el triángulo de lados 8, 6 y 10, y el siguiente, p = 5, con un triángulo 10, 24 y 26).
Si dibujamos radios donde la circunferencia toca con las diferentes partes del triángulo rectángulo, observamos que se puede construir dentro un triángulo rectángulo que comparte un ángulo con el original, de forma que son semejantes.
En el caso del triángulo de lados 6, 8 y 10, los dos lados sencillos de calcular serían r y 8 – r. La relación de semejanza podría ser (8 – r )/ r = 10/6, de donde se puede deducir que 10r = 48 – 6r, es decir 16r = 48 y r = 3. Es decir, que en el caso en que p = 3, r = 3.
En el de lados 10, 24 y 26, tendríamos que (24 – r)/r = 26/10, es decir, 240 – 10r = 26r, por lo que 240 = 36r y r = 20/3, no es un número entero.
En general, tenemos que (p² – 1 – r)/r = (p² + 1)/2p, por lo que 2p(p² – 1) – 2pr = (p² + 1)r. Dejando a un lado de la igualdad aquellos términos que llevan r, tendremos que 2p(p² – 1) = (p² + 1)r + 2pr.
Si sacamos factor común r, tendremos 2p(p² – 1) = (p² + 1+ 2p)r = (p + 1)²r.
De esta forma, r = 2p(p² – 1)/(p + 1)². Factorizando p² – 1 = (p + 1)(p – 1), y simplificando, r = 2p(p – 1)/(p + 1).
Vamos a analizar en qué valores de p este número puede ser entero. Si nos fijamos, p es un factor que no puede aparecer en la factorización de p + 1, por lo que dependerá de que se pueda simplificar 2(p – 1)/(p + 1). El factor 2 será simplificable seguro, ya que p + 1 es par, pero puesto que (p – 1)/(p +1) es menor que 1, la mitad de p + 1 debe coincidir exactamente con p – 1, cosa que sólo sucede en p = 3 (a partir de este valor, (p + 1)/ 2 es claramente mayor que p – 1.
Por lo tanto, el único valor de p para el que el radio es entero es p = 3.