Problema 1 del sábado de la Fase Local de la LV OME 2019 Se dirige a una edad de: 16-17 años
Considera el conjunto de números enteros positivos n cumpliendo 1 ≤ n ≤ 1000000.
En este conjunto, indica si es mayor la cantidad de números que pueden expresarse de la forma a³ + mb², con a, b números naturales y m pertenece al conjunto {0, 2, 4, 6, 8} o la cantidad de números que no pueden expresarse de esa manera.
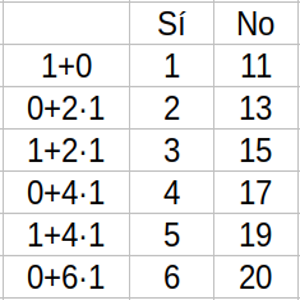
Solución:
Para los primeros números es fácil encontrar combinaciones de valores que dan, pero a partir del 11 la cosa se complica, de forma que no es fácil ir confeccionando la tabla, aunque se pueden crear rápidamente estrategias para desarrollarla.
Una manera fácil de abordar el problema es hacer una estimación al alza del número de valores que pueden lograrse mediante combinaciones de este tipo.
Puesto que 1000000 = 100³, hay como mucho 100 números que se puedan lograr como a³ + 0.
Si fijamos cualquier otro valor para m, puesto que como mucho hay 1000 cuadrados por debajo de 1000000, combinandolo con los 100 cubos, tendremos a lo sumo 100000 posibilidades (en realidad serán menos, ya que uno de los cubos es 1000000, y cualquier suma excede los números del conjunto).
Si sumamos la cantidad de números que hemos encontrado (entre los que habrá algunos repetidos, con lo que la cantidad real será menor) tenemos un total de 400100 números, y eso indica que hay más de 500900 números que no se podrán expresar de esta forma, de forma que se puede contestar con seguridad al enunciado, es mayor el conjunto de los que no se pueden expresar de la forma dicha.