Problema 4 de la Fase Local de la LVI OME 2020 Se dirige a una edad de: 16-17 años
Consideramos el siguiente polinomio para los valores reales a, b y c:
p(x) = (x – a)(x – b) + (x – b)(x – c) + (x – c)(x – a).
Demuestra que p(x) >= 0 para todo x real si y solamente si a = b = c.
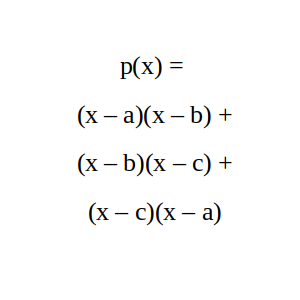
Solución:
Otro problema muy interesante de la fase local.
Está claro que hay que demostrar dos cosas. La más sencilla, es que si a = b = c, entonces, p(x) da valores no negativos.
La segunda, que si p(x) da valores no negativos, entonces a = b = c.
Veamos la primera. Al darse la igualdad, sustituyendo en la fórmula de p(x), tenemos que p(x) = (x – a)(x – a) + (x – a)(x – a) + (x – a)(x – a) = (x – a)² + (x – a)² + (x – a)² = 3(x – a)², que es claramente no negativo (3 es positivo y (x – a)² es no negativo por ser un número real al cuadrado.
Ahora bien, para demostrar la otra implicación hay que pensar un poco. Vamos a hacerlo por reducción al absurdo. Supongamos que no es cierta la afirmación. Entonces, puede que los tres números a, b, c sean diferentes, o que haya uno igual a otro y otro diferente de ambos.
La forma de llegar a una contradicción variará según estemos en un caso u otro.
Si los tres son diferentes, supongamos que a < b < c (dada la simetría de la fórmula de p(x), sería indiferente cualquier otro orden). Resulta que p(b) = (b – a)(b – b) + (b – b)(b – c) + (b – c)(b – a) = (b – c)(b – a) , pero b – c es negativo y b – a es positivo, por lo que el producto es p(b) y es negativo, de ahí la contradicción y el absurdo.
Luego los tres números no pueden ser diferentes. Ahora bien, si uno es diferente de los otros, pero ambos son iguales, supongamos que se da que a = b, pero c es diferente de los dos.
En ese caso, p(x) = (x – a)(x – a) + (x – a)(x – c) + (x – c)(x – a) = (x – a)² + 2(x – a)(x – c) = (x – a)(x – a + 2(x – c)), sacando factor común, es decir que p(x) = (x – a)(3x – a – 2c). Este polinomio, de segundo grado, tiene dos raíces, a y (a + 2c)/3. Evidentemente, son números diferentes. Si tomamos cualquier valor t entre ambos (por ejemplo, el valor medio, t = (4a + 2c)/6 = (2a + c)/3), al evaluar p(t) = (t – a)(3t – a – 2c) obtendríamos un número negativo, ya que uno de los dos factores sería positivo y el otro negativo (en el ejemplo, ((c – a)/3)(a – c) = (c – a)(a – c)/3 = -(a – c)²/3, que es negativo, ya que por ser a y c números diferentes, el cuadrado dividido por 3 es positivo, luego el signo lo vuelve negativo).
Alejandro Miralles nos propone otra idea muy interesante. Si llamamos q(x) = (x – a)(x – b)(x – c), es claro que p(x), como función, es la derivada de q(x). En ese caso, equivale decir que p(x) es no negativo a que q es no decreciente. Está claro que si a = b = c, q no es decreciente, y sin embargo, si hay dos que no son iguales, existen valores entre ambos en los que q es diferente de cero, por lo que en el intervalo entre ese valor y alguna de las raíces a, b o c, la función debe ser decreciente y por tanto p(x) debe ser negativo en ese intervalo.