Problema 2 de la fase nacional de la 57 Olimpiada Matemática Española (2021)
Se dirige a una edad de: 16-17 años

Dado un número entero positivo n, definimos λ(n) como el número de soluciones enteras positivas de la ecuación x² – y² = n.

Diremos que el número n es “olímpico” si λ(n) = 2021.

¿Cuál es el primer entero positivo que es olímpico?

¿Y cuál es el menor entero positivo impar que es olímpico?

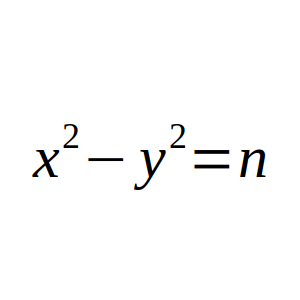
Solución:

La clave en los problemas con enteros suele ser escribir sus factores. Si vemos la ecuación de la que debemos encontrar las soluciones enteras, es x² – y² = n, es decir, (x + y)(x – y) = n.

Estudiemos el número de soluciones x, y que vamos a encontrar para un entero dado.

Imaginemos algo como n = 5, y contemos.

Veamos un ejemplo, 5 sólo tiene los divisores 5 y 1, y por tanto, puesto que necesariamente x – y es menor que x + y, tendremos que x – y = 1 y x + y = 5, de donde 2x = 6 y 2y = 4, es decir, x = 3 e y = 2 es la única solución (en efecto, 9 – 4 = 5).

Probemos otro, 12 tiene 6 divisores, 12, 6, 4, 3, 2, 1. Es decir, que 12 puede escribirse de tres formas diferentes, si tenemos en cuenta que uno de los factores necesariamente es mayor que otro. Tenemos que 12·1 = 12, 6·2 = 12 y 4·3 = 12. Sin embargo, x + y y x – y son dos números que presentan la misma paridad, de forma que los productos 12·1 y 4·3 quedan descartados, sólo tendríamos la solución que aporte la factorización 6·2, que será que x = 4 e y = 2.

En general, el número de soluciones de la ecuación coincide con el número de factorizaciones de n en dos factores en la que ambos factores tienen la misma paridad, ya que es necesario y suficiente que tengan la misma paridad (si no tienen la misma paridad no existe x e y, y si tienen la misma existen seguro).

Hay que tener en cuenta por separado la posibilidad de que el numero n sea un cuadrado perfecto, ya que en ese caso el número de divisores es impar, y hay uno de ellos que no produce ninguna solución en la ecuación, ya que x – y no puede ser igual a x + y si ambos son enteros positivos.

Empecemos con la versión fácil, si n es impar y no es un cuadrado, todos sus divisores son impares, con lo que el número de soluciones de la ecuación x² – y² = n coincide con la mitad de los factores.

Puesto que es posible calcular el número de factores a partir de la descomposición factorial, podemos conocer cuál es el primero eligiendo cuidadosamente los factores primos que forman n.

Por ejemplo, si tenemos un valor de n = 3⁵·5²·7, la cantidad de divisores sería de (5 + 1)·(2 + 1)·(1 + 1) = 6·3·2 = 36. Y entonces, λ(n) sería 18. Es decir, la forma de calcular la cantidad de divisores sería multiplicar todos los exponentes de los factores primos aumentados en 1. Y calcular λ(n) sería tan sencillo como dividir por 2.

Pero no sólo nos permite saber el número de divisores, la descomposición en factores primos nos permite construir todos esos divisores.

Puesto que 2021 es 43·47, para que λ(n) = 2021, debería darse que el número de divisores fuese 43·47·2, y la forma más baja de lograrlo sería con el número 3⁴⁶·5⁴²·7. Es decir, el número olímpico impar más bajo sería 3⁴⁶·5⁴²·7. Este número es enorme, 14106391708439220490505022098659537732601165771484375 y evidentemente no hay que calcularlo de forma explícita.

Veamos ahora qué pasa con los pares. De todos los divisores posibles, deberíamos eliminar todos los que, o bien no tengan ningún factor par (ya que todos los factores pares se concentrarían en el otro), o bien los tengan todos, con los que el menor que daría 2021 como resultado será 2⁴⁸·3⁴²·5, ya que sus divisores aceptables para obtener soluciones, una vez eliminados los que tengan diferente paridad serían (49·43·2 – 2·43·2) = 47·43·2, por lo que λ(n) = 2021.

Este número sí sería el más bajo de los olímpicos, y sería 153993537087479816461503505650155520, que es bastante inferior (no es conveniente calcularlo de forma explícita).

Trabajar con los cuadrados sería más difícil, ya que el número de divisores que buscaríamos no sería 2021·2 = 4042, si no 4043. y este número es 13·311, con lo que hablaríamos de un número mucho más grande. De hecho, el primer impar cuadrado sería 3³¹⁰·5¹², que sería muy superior a los números de los que nos hemos ocupado, y el primer par sería 2³¹²·3¹², que también sería muy grande (superior también a los números tratados).