Problema 2 de la fase catalana de la 57 Olimpiada Matemática Española (2020/21)
Se dirige a una edad de: 16-17 años

Tenemos un tablero nxn, con n > 2.

Escribimos en cada casilla un número natural entre el 1 y el n² diferente, en cualquier orden.

Demuestra que siempre existen dos casillas adyacentes tales que los números que x, y que contienen satisfacen la siguiente desigualdad: |x – y| ≥ n/2 + 1.

Entendemos que son casillas adyacentes aquellas que comparten un lado.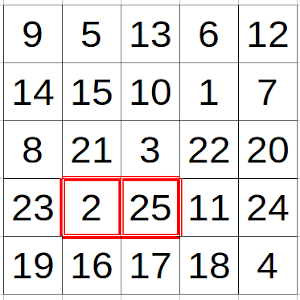
Solución: Aquí.